Guillaume Balarac
Gradient-free online learning of subgrid-scale dynamics with neural emulators
Nov 02, 2023



Abstract:In this paper, we propose a generic algorithm to train machine learning-based subgrid parametrizations online, i.e., with $\textit{a posteriori}$ loss functions for non-differentiable numerical solvers. The proposed approach leverage neural emulators to train an approximation of the reduced state-space solver, which is then used to allows gradient propagation through temporal integration steps. The algorithm is able to recover most of the benefit of online strategies without having to compute the gradient of the original solver. It is demonstrated that training the neural emulator and parametrization components separately with respective loss quantities is necessary in order to minimize the propagation of some approximation bias.
A posteriori learning for quasi-geostrophic turbulence parametrization
Apr 08, 2022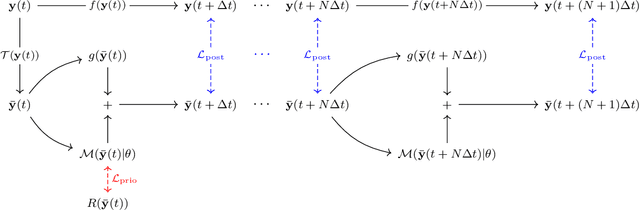

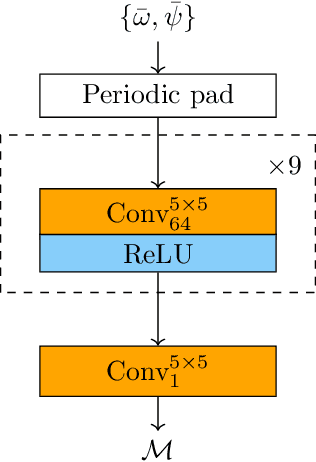
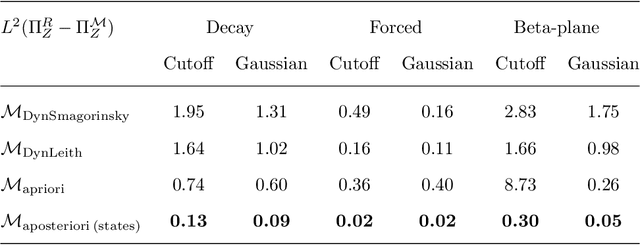
Abstract:The use of machine learning to build subgrid parametrizations for climate models is receiving growing attention. State-of-the-art strategies address the problem as a supervised learning task and optimize algorithms that predict subgrid fluxes based on information from coarse resolution models. In practice, training data are generated from higher resolution numerical simulations transformed in order to mimic coarse resolution simulations. By essence, these strategies optimize subgrid parametrizations to meet so-called $\textit{a priori}$ criteria. But the actual purpose of a subgrid parametrization is to obtain good performance in terms of $\textit{a posteriori}$ metrics which imply computing entire model trajectories. In this paper, we focus on the representation of energy backscatter in two dimensional quasi-geostrophic turbulence and compare parametrizations obtained with different learning strategies at fixed computational complexity. We show that strategies based on $\textit{a priori}$ criteria yield parametrizations that tend to be unstable in direct simulations and describe how subgrid parametrizations can alternatively be trained end-to-end in order to meet $\textit{a posteriori}$ criteria. We illustrate that end-to-end learning strategies yield parametrizations that outperform known empirical and data-driven schemes in terms of performance, stability and ability to apply to different flow configurations. These results support the relevance of differentiable programming paradigms for climate models in the future.
A posteriori learning of quasi-geostrophic turbulence parametrization: an experiment on integration steps
Nov 27, 2021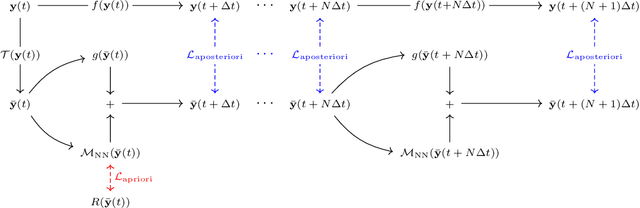


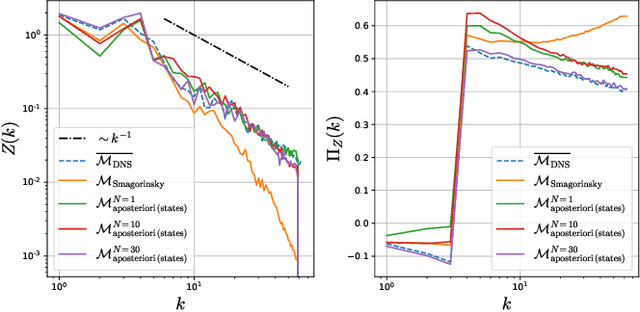
Abstract:Modeling the subgrid-scale dynamics of reduced models is a long standing open problem that finds application in ocean, atmosphere and climate predictions where direct numerical simulation (DNS) is impossible. While neural networks (NNs) have already been applied to a range of three-dimensional flows with success, two dimensional flows are more challenging because of the backscatter of energy from small to large scales. We show that learning a model jointly with the dynamical solver and a meaningful \textit{a posteriori}-based loss function lead to stable and realistic simulations when applied to quasi-geostrophic turbulence.
Physical invariance in neural networks for subgrid-scale scalar flux modeling
Oct 09, 2020



Abstract:In this paper we present a new strategy to model the subgrid-scale scalar flux in a three-dimensional turbulent incompressible flow using physics-informed neural networks (NNs). When trained from direct numerical simulation (DNS) data, state-of-the-art neural networks, such as convolutional neural networks, may not preserve well known physical priors, which may in turn question their application to real case-studies. To address this issue, we investigate hard and soft constraints into the model based on classical invariances and symmetries derived from physical laws. From simulation-based experiments, we show that the proposed physically-invariant NN model outperforms both purely data-driven ones as well as parametric state-of-the-art subgrid-scale model. The considered invariances are regarded as regularizers on physical metrics during the a priori evaluation and constrain the distribution tails of the predicted subgrid-scale term to be closer to the DNS. They also increase the stability and performance of the model when used as a surrogate during a large-eddy simulation. Moreover, the physically-invariant NN is shown to generalize to configurations that have not been seen during the training phase.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge