A posteriori learning of quasi-geostrophic turbulence parametrization: an experiment on integration steps
Paper and Code
Nov 27, 2021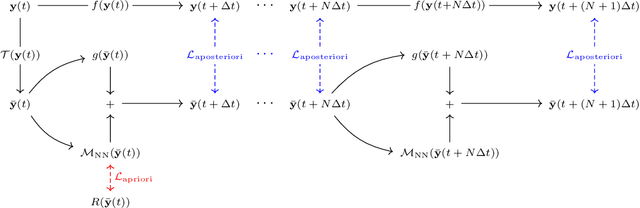


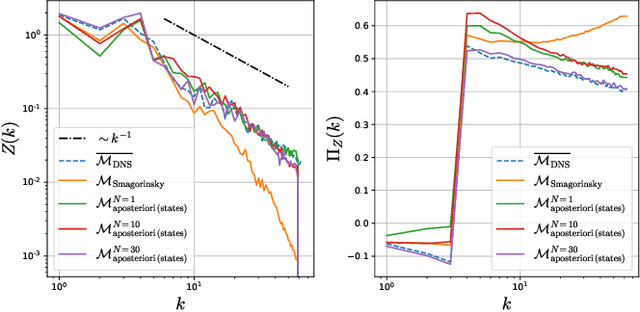
Modeling the subgrid-scale dynamics of reduced models is a long standing open problem that finds application in ocean, atmosphere and climate predictions where direct numerical simulation (DNS) is impossible. While neural networks (NNs) have already been applied to a range of three-dimensional flows with success, two dimensional flows are more challenging because of the backscatter of energy from small to large scales. We show that learning a model jointly with the dynamical solver and a meaningful \textit{a posteriori}-based loss function lead to stable and realistic simulations when applied to quasi-geostrophic turbulence.
* 6 pages, 3 figures, presented at the Fourth Workshop on Machine
Learning and the Physical Sciences (NeurIPS 2021)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge