Strictly Constrained Generative Modeling via Split Augmented Langevin Sampling

Deep generative models hold great promise for representing complex physical systems, but their deployment is currently limited by the lack of guarantees on the physical plausibility of the generated outputs. Ensuring that known physical constraints are enforced is therefore critical when applying generative models to scientific and engineering problems. We address this limitation by developing a principled framework for sampling from a target distribution while rigorously satisfying physical constraints. Leveraging the variational formulation of Langevin dynamics, we propose Split Augmented Langevin (SAL), a novel primal-dual sampling algorithm that enforces constraints progressively through variable splitting, with convergence guarantees. While the method is developed theoretically for Langevin dynamics, we demonstrate its effective applicability to diffusion models. In particular, we use constrained diffusion models to generate physical fields satisfying energy and mass conservation laws. We apply our method to diffusion-based data assimilation on a complex physical system, where enforcing physical constraints substantially improves both forecast accuracy and the preservation of critical conserved quantities. We also demonstrate the potential of SAL for challenging feasibility problems in optimal control.

Neural Incremental Data Assimilation

Data assimilation is a central problem in many geophysical applications, such as weather forecasting. It aims to estimate the state of a potentially large system, such as the atmosphere, from sparse observations, supplemented by prior physical knowledge. The size of the systems involved and the complexity of the underlying physical equations make it a challenging task from a computational point of view. Neural networks represent a promising method of emulating the physics at low cost, and therefore have the potential to considerably improve and accelerate data assimilation. In this work, we introduce a deep learning approach where the physical system is modeled as a sequence of coarse-to-fine Gaussian prior distributions parametrized by a neural network. This allows us to define an assimilation operator, which is trained in an end-to-end fashion to minimize the reconstruction error on a dataset with different observation processes. We illustrate our approach on chaotic dynamical physical systems with sparse observations, and compare it to traditional variational data assimilation methods.

Interpretable Meta-Learning of Physical Systems

Machine learning methods can be a valuable aid in the scientific process, but they need to face challenging settings where data come from inhomogeneous experimental conditions. Recent meta-learning methods have made significant progress in multi-task learning, but they rely on black-box neural networks, resulting in high computational costs and limited interpretability. Leveraging the structure of the learning problem, we argue that multi-environment generalization can be achieved using a simpler learning model, with an affine structure with respect to the learning task. Crucially, we prove that this architecture can identify the physical parameters of the system, enabling interpreable learning. We demonstrate the competitive generalization performance and the low computational cost of our method by comparing it to state-of-the-art algorithms on physical systems, ranging from toy models to complex, non-analytical systems. The interpretability of our method is illustrated with original applications to physical-parameter-induced adaptation and to adaptive control.

FLEX: an Adaptive Exploration Algorithm for Nonlinear Systems

Model-based reinforcement learning is a powerful tool, but collecting data to fit an accurate model of the system can be costly. Exploring an unknown environment in a sample-efficient manner is hence of great importance. However, the complexity of dynamics and the computational limitations of real systems make this task challenging. In this work, we introduce FLEX, an exploration algorithm for nonlinear dynamics based on optimal experimental design. Our policy maximizes the information of the next step and results in an adaptive exploration algorithm, compatible with generic parametric learning models and requiring minimal resources. We test our method on a number of nonlinear environments covering different settings, including time-varying dynamics. Keeping in mind that exploration is intended to serve an exploitation objective, we also test our algorithm on downstream model-based classical control tasks and compare it to other state-of-the-art model-based and model-free approaches. The performance achieved by FLEX is competitive and its computational cost is low.

Online greedy identification of linear dynamical systems

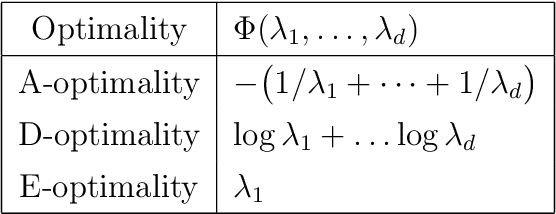
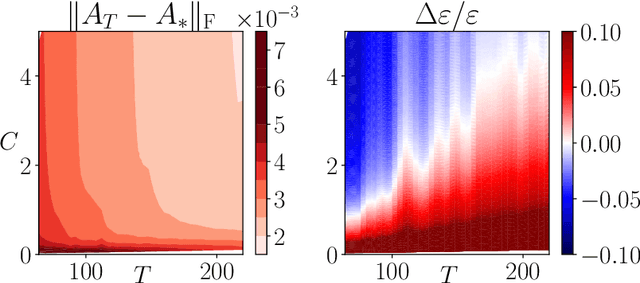
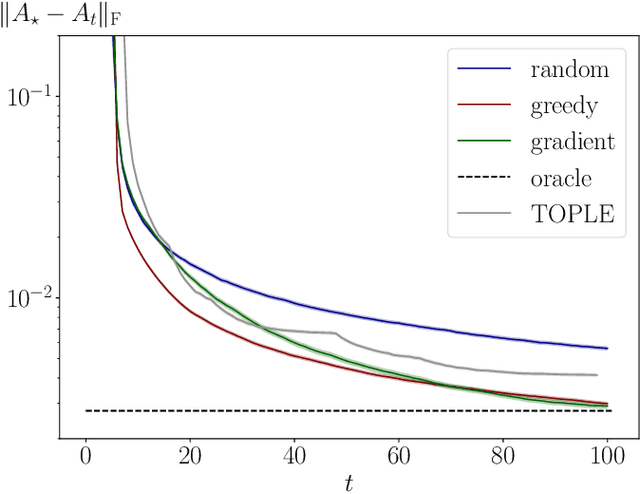
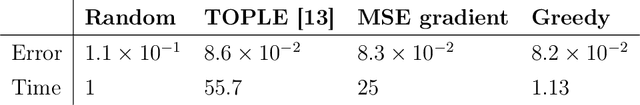
This work addresses the problem of exploration in an unknown environment. For linear dynamical systems, we use an experimental design framework and introduce an online greedy policy where the control maximizes the information of the next step. In a setting with a limited number of experimental trials, our algorithm has low complexity and shows experimentally competitive performances compared to more elaborate gradient-based methods.