Global Convergence of Model Function Based Bregman Proximal Minimization Algorithms

Lipschitz continuity of the gradient mapping of a continuously differentiable function plays a crucial role in designing various optimization algorithms. However, many functions arising in practical applications such as low rank matrix factorization or deep neural network problems do not have a Lipschitz continuous gradient. This led to the development of a generalized notion known as the $L$-smad property, which is based on generalized proximity measures called Bregman distances. However, the $L$-smad property cannot handle nonsmooth functions, for example, simple nonsmooth functions like $\abs{x^4-1}$ and also many practical composite problems are out of scope. We fix this issue by proposing the MAP property, which generalizes the $L$-smad property and is also valid for a large class of nonconvex nonsmooth composite problems. Based on the proposed MAP property, we propose a globally convergent algorithm called Model BPG, that unifies several existing algorithms. The convergence analysis is based on a new Lyapunov function. We also numerically illustrate the superior performance of Model BPG on standard phase retrieval problems, robust phase retrieval problems, and Poisson linear inverse problems, when compared to a state of the art optimization method that is valid for generic nonconvex nonsmooth optimization problems.

Bregman Proximal Framework for Deep Linear Neural Networks

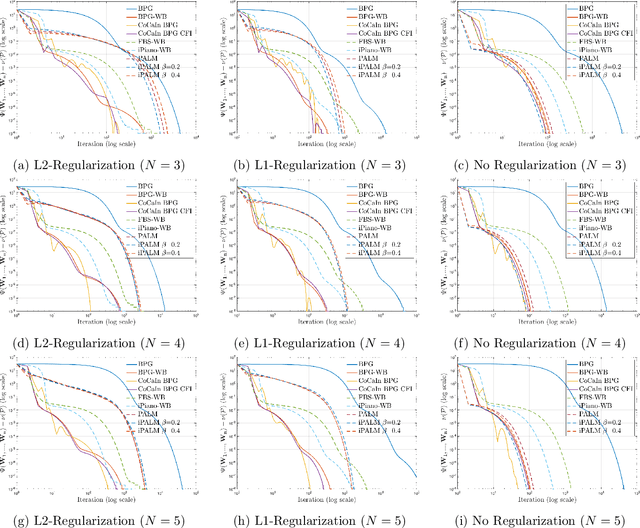
A typical assumption for the analysis of first order optimization methods is the Lipschitz continuity of the gradient of the objective function. However, for many practical applications this assumption is violated, including loss functions in deep learning. To overcome this issue, certain extensions based on generalized proximity measures known as Bregman distances were introduced. This initiated the development of the Bregman proximal gradient (BPG) algorithm and an inertial variant (momentum based) CoCaIn BPG, which however rely on problem dependent Bregman distances. In this paper, we develop Bregman distances for using BPG methods to train Deep Linear Neural Networks. The main implications of our results are strong convergence guarantees for these algorithms. We also propose several strategies for their efficient implementation, for example, closed form updates and a closed form expression for the inertial parameter of CoCaIn BPG. Moreover, the BPG method requires neither diminishing step sizes nor line search, unlike its corresponding Euclidean version. We numerically illustrate the competitiveness of the proposed methods compared to existing state of the art schemes.

Beyond Alternating Updates for Matrix Factorization with Inertial Bregman Proximal Gradient Algorithms

Matrix Factorization is a popular non-convex objective, for which alternating minimization schemes are mostly used. They usually suffer from the major drawback that the solution is biased towards one of the optimization variables. A remedy is non-alternating schemes. However, due to a lack of Lipschitz continuity of the gradient in matrix factorization problems, convergence cannot be guaranteed. A recently developed remedy relies on the concept of Bregman distances, which generalizes the standard Euclidean distance. We exploit this theory by proposing a novel Bregman distance for matrix factorization problems, which, at the same time, allows for simple/closed form update steps. Therefore, for non-alternating schemes, such as the recently introduced Bregman Proximal Gradient (BPG) method and an inertial variant Convex--Concave Inertial BPG (CoCaIn BPG), convergence of the whole sequence to a stationary point is proved for Matrix Factorization. In several experiments, we observe a superior performance of our non-alternating schemes in terms of speed and objective value at the limit point.

Convex-Concave Backtracking for Inertial Bregman Proximal Gradient Algorithms in Non-Convex Optimization

Backtracking line-search is an old yet powerful strategy for finding better step size to be used in proximal gradient algorithms. The main principle is to locally find a simple convex upper bound of the objective function, which in turn controls the step size that is used. In case of inertial proximal gradient algorithms, the situation becomes much more difficult and usually leads to very restrictive rules on the extrapolation parameter. In this paper, we show that the extrapolation parameter can be controlled by locally finding also a simple concave lower bound of the objective function. This gives rise to a double convex-concave backtracking procedure which allows for an adaptive and optimal choice of both the step size and extrapolation parameters. We apply this procedure to the class of inertial Bregman proximal gradient methods, and prove that any sequence generated converges globally to critical points of the function at hand. Numerical experiments on a number of challenging non-convex problems in image processing and machine learning were conducted and show the power of combining inertial step and double backtracking strategy in achieving improved performances.

On the loss landscape of a class of deep neural networks with no bad local valleys

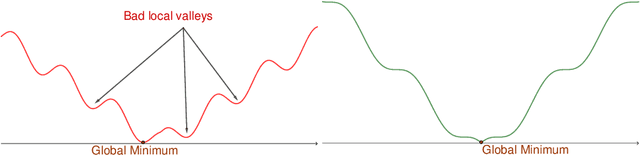
We identify a class of over-parameterized deep neural networks with standard activation functions and cross-entropy loss which provably have no bad local valley, in the sense that from any point in parameter space there exists a continuous path on which the cross-entropy loss is non-increasing and gets arbitrarily close to zero. This implies that these networks have no sub-optimal strict local minima.

Neural Networks Should Be Wide Enough to Learn Disconnected Decision Regions

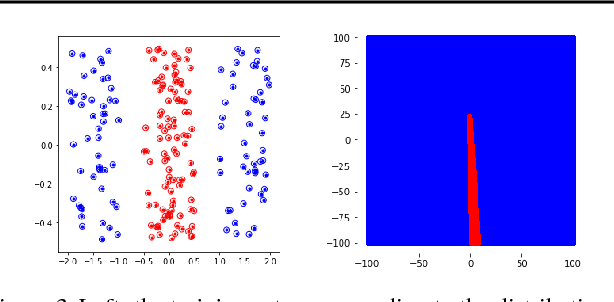
In the recent literature the important role of depth in deep learning has been emphasized. In this paper we argue that sufficient width of a feedforward network is equally important by answering the simple question under which conditions the decision regions of a neural network are connected. It turns out that for a class of activation functions including leaky ReLU, neural networks having a pyramidal structure, that is no layer has more hidden units than the input dimension, produce necessarily connected decision regions. This implies that a sufficiently wide hidden layer is necessary to guarantee that the network can produce disconnected decision regions. We discuss the implications of this result for the construction of neural networks, in particular the relation to the problem of adversarial manipulation of classifiers.

Variants of RMSProp and Adagrad with Logarithmic Regret Bounds

Adaptive gradient methods have become recently very popular, in particular as they have been shown to be useful in the training of deep neural networks. In this paper we have analyzed RMSProp, originally proposed for the training of deep neural networks, in the context of online convex optimization and show $\sqrt{T}$-type regret bounds. Moreover, we propose two variants SC-Adagrad and SC-RMSProp for which we show logarithmic regret bounds for strongly convex functions. Finally, we demonstrate in the experiments that these new variants outperform other adaptive gradient techniques or stochastic gradient descent in the optimization of strongly convex functions as well as in training of deep neural networks.