How to Build Robust, Scalable Models for GSV-Based Indicators in Neighborhood Research

A substantial body of health research demonstrates a strong link between neighborhood environments and health outcomes. Recently, there has been increasing interest in leveraging advances in computer vision to enable large-scale, systematic characterization of neighborhood built environments. However, the generalizability of vision models across fundamentally different domains remains uncertain, for example, transferring knowledge from ImageNet to the distinct visual characteristics of Google Street View (GSV) imagery. In applied fields such as social health research, several critical questions arise: which models are most appropriate, whether to adopt unsupervised training strategies, what training scale is feasible under computational constraints, and how much such strategies benefit downstream performance. These decisions are often costly and require specialized expertise. In this paper, we answer these questions through empirical analysis and provide practical insights into how to select and adapt foundation models for datasets with limited size and labels, while leveraging larger, unlabeled datasets through unsupervised training. Our study includes comprehensive quantitative and visual analyses comparing model performance before and after unsupervised adaptation.

Weak-to-Strong Generalization Enables Fully Automated De Novo Training of Multi-head Mask-RCNN Model for Segmenting Densely Overlapping Cell Nuclei in Multiplex Whole-slice Brain Images

We present a weak to strong generalization methodology for fully automated training of a multi-head extension of the Mask-RCNN method with efficient channel attention for reliable segmentation of overlapping cell nuclei in multiplex cyclic immunofluorescent (IF) whole-slide images (WSI), and present evidence for pseudo-label correction and coverage expansion, the key phenomena underlying weak to strong generalization. This method can learn to segment de novo a new class of images from a new instrument and/or a new imaging protocol without the need for human annotations. We also present metrics for automated self-diagnosis of segmentation quality in production environments, where human visual proofreading of massive WSI images is unaffordable. Our method was benchmarked against five current widely used methods and showed a significant improvement. The code, sample WSI images, and high-resolution segmentation results are provided in open form for community adoption and adaptation.

DualProtoSeg: Simple and Efficient Design with Text- and Image-Guided Prototype Learning for Weakly Supervised Histopathology Image Segmentation

Weakly supervised semantic segmentation (WSSS) in histopathology seeks to reduce annotation cost by learning from image-level labels, yet it remains limited by inter-class homogeneity, intra-class heterogeneity, and the region-shrinkage effect of CAM-based supervision. We propose a simple and effective prototype-driven framework that leverages vision-language alignment to improve region discovery under weak supervision. Our method integrates CoOp-style learnable prompt tuning to generate text-based prototypes and combines them with learnable image prototypes, forming a dual-modal prototype bank that captures both semantic and appearance cues. To address oversmoothing in ViT representations, we incorporate a multi-scale pyramid module that enhances spatial precision and improves localization quality. Experiments on the BCSS-WSSS benchmark show that our approach surpasses existing state-of-the-art methods, and detailed analyses demonstrate the benefits of text description diversity, context length, and the complementary behavior of text and image prototypes. These results highlight the effectiveness of jointly leveraging textual semantics and visual prototype learning for WSSS in digital pathology.

TaDeR: A New Task Dependency Recommendation for Project Management Platform

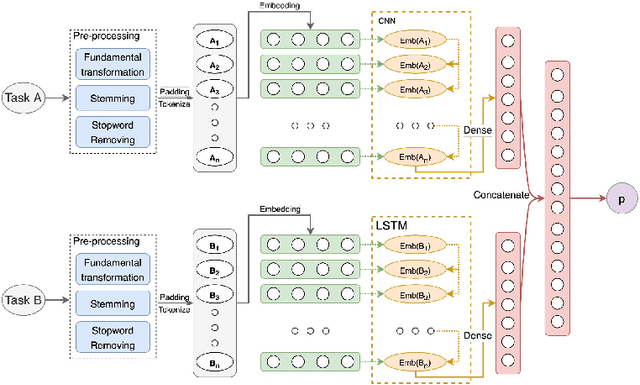
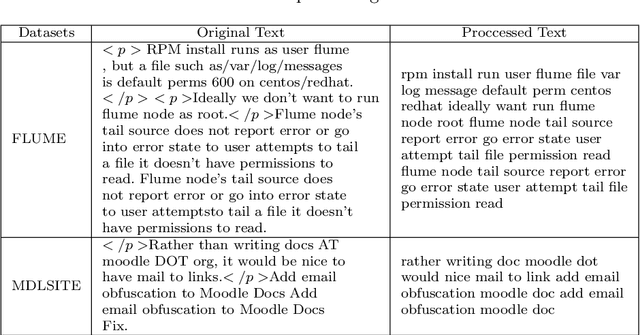
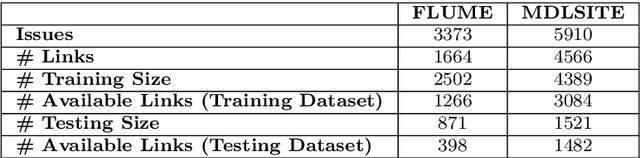
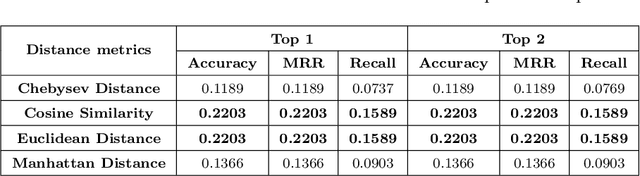
Many startups and companies worldwide have been using project management software and tools to monitor, track and manage their projects. For software projects, the number of tasks from the beginning to the end is quite a large number that sometimes takes a lot of time and effort to search and link the current task to a group of previous ones for further references. This paper proposes an efficient task dependency recommendation algorithm to suggest tasks dependent on a given task that the user has just created. We present an efficient feature engineering step and construct a deep neural network to this aim. We performed extensive experiments on two different large projects (MDLSITE from moodle.org and FLUME from apache.org) to find the best features in 28 combinations of features and the best performance model using two embedding methods (GloVe and FastText). We consider three types of models (GRU, CNN, LSTM) using Accuracy@K, MRR@K, and Recall@K (where K = 1, 2, 3, and 5) and baseline models using traditional methods: TF-IDF with various matching score calculating such as cosine similarity, Euclidean distance, Manhattan distance, and Chebyshev distance. After many experiments, the GloVe Embedding and CNN model reached the best result in our dataset, so we chose this model as our proposed method. In addition, adding the time filter in the post-processing step can significantly improve the recommendation system's performance. The experimental results show that our proposed method can reach 0.2335 in Accuracy@1 and MRR@1 and 0.2011 in Recall@1 of dataset FLUME. With the MDLSITE dataset, we obtained 0.1258 in Accuracy@1 and MRR@1 and 0.1141 in Recall@1. In the top 5, our model reached 0.3040 in Accuracy@5, 0.2563 MRR@5, and 0.2651 Recall@5 in FLUME. In the MDLSITE dataset, our model got 0.5270 Accuracy@5, 0.2689 MRR@5, and 0.2651 Recall@5.

On Connectivity of Solutions in Deep Learning: The Role of Over-parameterization and Feature Quality

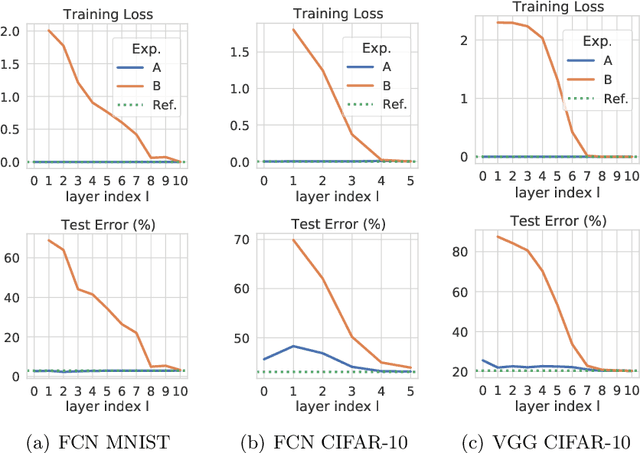
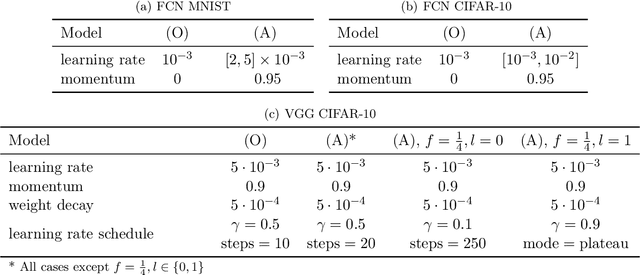
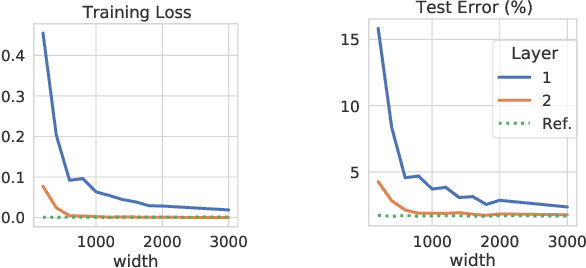
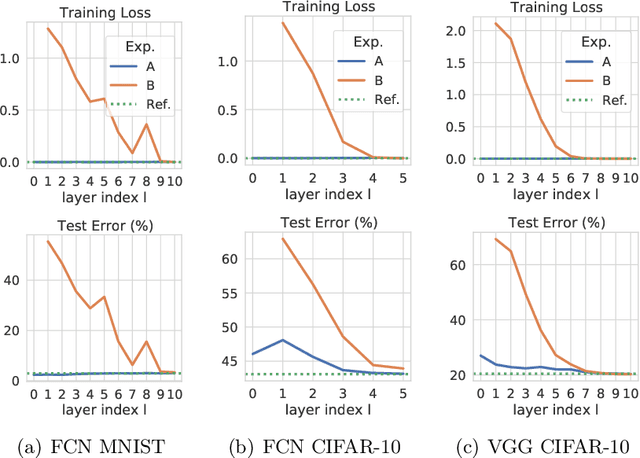
It has been empirically observed that, in deep neural networks, the solutions found by stochastic gradient descent from different random initializations can be often connected by a path with low loss. Recent works have shed light on this intriguing phenomenon by assuming either the over-parameterization of the network or the dropout stability of the solutions. In this paper, we reconcile these two views and present a novel condition for ensuring the connectivity of two arbitrary points in parameter space. This condition is provably milder than dropout stability, and it provides a connection between the problem of finding low-loss paths and the memorization capacity of neural nets. This last point brings about a trade-off between the quality of features at each layer and the over-parameterization of the network. As an extreme example of this trade-off, we show that (i) if subsets of features at each layer are linearly separable, then almost no over-parameterization is needed, and (ii) under generic assumptions on the features at each layer, it suffices that the last two hidden layers have $\Omega(\sqrt{N})$ neurons, $N$ being the number of samples. Finally, we provide experimental evidence demonstrating that the presented condition is satisfied in practical settings even when dropout stability does not hold.

On the Proof of Global Convergence of Gradient Descent for Deep ReLU Networks with Linear Widths

This paper studies the global convergence of gradient descent for deep ReLU networks under the square loss. For this setting, the current state-of-the-art results show that gradient descent converges to a global optimum if the widths of all the hidden layers scale at least as $\Omega(N^8)$ ($N$ being the number of training samples). In this paper, we discuss a simple proof framework which allows us to improve the existing over-parameterization condition to linear, quadratic and cubic widths (depending on the type of initialization scheme and/or the depth of the network).

A Fully Rigorous Proof of the Derivation of Xavier and He's Initialization for Deep ReLU Networks

A fully rigorous proof of the derivation of Xavier/He's initialization for ReLU nets is given.

A Note on Connectivity of Sublevel Sets in Deep Learning

It is shown that for deep neural networks, a single wide layer of width $N+1$ ($N$ being the number of training samples) suffices to prove the connectivity of sublevel sets of the training loss function. In the two-layer setting, the same property may not hold even if one has just one neuron less (i.e. width $N$ can lead to disconnected sublevel sets).

Tight Bounds on the Smallest Eigenvalue of the Neural Tangent Kernel for Deep ReLU Networks

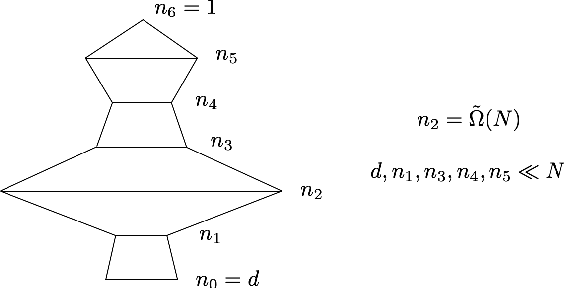
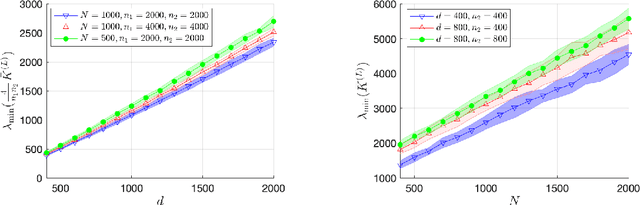
A recent line of work has analyzed the theoretical properties of deep neural networks via the Neural Tangent Kernel (NTK). In particular, the smallest eigenvalue of the NTK has been related to memorization capacity, convergence of gradient descent algorithms and generalization of deep nets. However, existing results either provide bounds in the two-layer setting or assume that the spectrum of the NTK is bounded away from 0 for multi-layer networks. In this paper, we provide tight bounds on the smallest eigenvalue of NTK matrices for deep ReLU networks, both in the limiting case of infinite widths and for finite widths. In the finite-width setting, the network architectures we consider are quite general: we require the existence of a wide layer with roughly order of $N$ neurons, $N$ being the number of data samples; and the scaling of the remaining widths is arbitrary (up to logarithmic factors). To obtain our results, we analyze various quantities of independent interest: we give lower bounds on the smallest singular value of feature matrices, and upper bounds on the Lipschitz constant of input-output feature maps.

Global Convergence of Deep Networks with One Wide Layer Followed by Pyramidal Topology

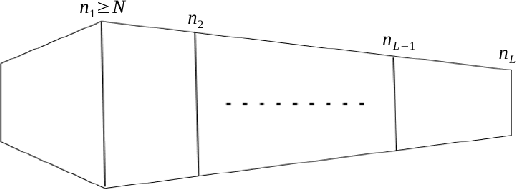
A recent line of research has provided convergence guarantees for gradient descent algorithms in the excessive over-parameterization regime where the widths of all the hidden layers are required to be polynomially large in the number of training samples. However, the widths of practical deep networks are often only large in the first layer(s) and then start to decrease towards the output layer. This raises an interesting open question whether similar results also hold under this empirically relevant setting. Existing theoretical insights suggest that the loss surface of this class of networks is well-behaved, but these results usually do not provide direct algorithmic guarantees for optimization. In this paper, we close the gap by showing that one wide layer followed by pyramidal deep network topology suffices for gradient descent to find a global minimum with a geometric rate. Our proof is based on a weak form of Polyak-Lojasiewicz inequality which holds for deep pyramidal networks in the manifold of full-rank weight matrices.