Adaptive Certified Training: Towards Better Accuracy-Robustness Tradeoffs

As deep learning models continue to advance and are increasingly utilized in real-world systems, the issue of robustness remains a major challenge. Existing certified training methods produce models that achieve high provable robustness guarantees at certain perturbation levels. However, the main problem of such models is a dramatically low standard accuracy, i.e. accuracy on clean unperturbed data, that makes them impractical. In this work, we consider a more realistic perspective of maximizing the robustness of a model at certain levels of (high) standard accuracy. To this end, we propose a novel certified training method based on a key insight that training with adaptive certified radii helps to improve both the accuracy and robustness of the model, advancing state-of-the-art accuracy-robustness tradeoffs. We demonstrate the effectiveness of the proposed method on MNIST, CIFAR-10, and TinyImageNet datasets. Particularly, on CIFAR-10 and TinyImageNet, our method yields models with up to two times higher robustness, measured as an average certified radius of a test set, at the same levels of standard accuracy compared to baseline approaches.

Universe Points Representation Learning for Partial Multi-Graph Matching

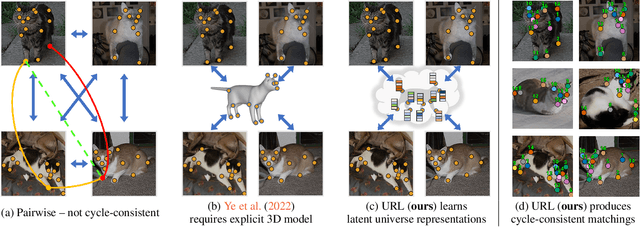
Many challenges from natural world can be formulated as a graph matching problem. Previous deep learning-based methods mainly consider a full two-graph matching setting. In this work, we study the more general partial matching problem with multi-graph cycle consistency guarantees. Building on a recent progress in deep learning on graphs, we propose a novel data-driven method (URL) for partial multi-graph matching, which uses an object-to-universe formulation and learns latent representations of abstract universe points. The proposed approach advances the state of the art in semantic keypoint matching problem, evaluated on Pascal VOC, CUB, and Willow datasets. Moreover, the set of controlled experiments on a synthetic graph matching dataset demonstrates the scalability of our method to graphs with large number of nodes and its robustness to high partiality.

Neural Network Virtual Sensors for Fuel Injection Quantities with Provable Performance Specifications

Recent work has shown that it is possible to learn neural networks with provable guarantees on the output of the model when subject to input perturbations, however these works have focused primarily on defending against adversarial examples for image classifiers. In this paper, we study how these provable guarantees can be naturally applied to other real world settings, namely getting performance specifications for robust virtual sensors measuring fuel injection quantities within an engine. We first demonstrate that, in this setting, even simple neural network models are highly susceptible to reasonable levels of adversarial sensor noise, which are capable of increasing the mean relative error of a standard neural network from 6.6% to 43.8%. We then leverage methods for learning provably robust networks and verifying robustness properties, resulting in a robust model which we can provably guarantee has at most 16.5% mean relative error under any sensor noise. Additionally, we show how specific intervals of fuel injection quantities can be targeted to maximize robustness for certain ranges, allowing us to train a virtual sensor for fuel injection which is provably guaranteed to have at most 10.69% relative error under noise while maintaining 3% relative error on non-adversarial data within normalized fuel injection ranges of 0.6 to 1.0.

Adversarial camera stickers: A physical camera-based attack on deep learning systems

Recent work has thoroughly documented the susceptibility of deep learning systems to adversarial examples, but most such instances directly manipulate the digital input to a classifier. Although a smaller line of work considers physical adversarial attacks, in all cases these involve manipulating the object of interest, e.g., putting a physical sticker on a object to misclassify it, or manufacturing an object specifically intended to be misclassified. In this work, we consider an alternative question: is it possible to fool deep classifiers, over all perceived objects of a certain type, by physically manipulating the camera itself? We show that this is indeed possible, that by placing a carefully crafted and mainly-translucent sticker over the lens of a camera, one can create universal perturbations of the observed images that are inconspicuous, yet reliably misclassify target objects as a different (targeted) class. To accomplish this, we propose an iterative procedure for both updating the attack perturbation (to make it adversarial for a given classifier), and the threat model itself (to ensure it is physically realizable). For example, we show that we can achieve physically-realizable attacks that fool ImageNet classifiers in a targeted fashion 49.6% of the time. This presents a new class of physically-realizable threat models to consider in the context of adversarially robust machine learning. Our demo video can be viewed at: https://youtu.be/wUVmL33Fx54

Wasserstein Adversarial Examples via Projected Sinkhorn Iterations

A rapidly growing area of work has studied the existence of adversarial examples, datapoints which have been perturbed to fool a classifier, but the vast majority of these works have focused primarily on threat models defined by $\ell_p$ norm-bounded perturbations. In this paper, we propose a new threat model for adversarial attacks based on the Wasserstein distance. In the image classification setting, such distances measure the cost of moving pixel mass, which naturally cover "standard" image manipulations such as scaling, rotation, translation, and distortion (and can potentially be applied to other settings as well). To generate Wasserstein adversarial examples, we develop a procedure for projecting onto the Wasserstein ball, based upon a modified version of the Sinkhorn iteration. The resulting algorithm can successfully attack image classification models, bringing traditional CIFAR10 models down to 3% accuracy within a Wasserstein ball with radius 0.1 (i.e., moving 10% of the image mass 1 pixel), and we demonstrate that PGD-based adversarial training can improve this adversarial accuracy to 76%. In total, this work opens up a new direction of study in adversarial robustness, more formally considering convex metrics that accurately capture the invariances that we typically believe should exist in classifiers. Code for all experiments in the paper is available at https://github.com/locuslab/projected_sinkhorn.

Discrete-Continuous ADMM for Transductive Inference in Higher-Order MRFs

This paper introduces a novel algorithm for transductive inference in higher-order MRFs, where the unary energies are parameterized by a variable classifier. The considered task is posed as a joint optimization problem in the continuous classifier parameters and the discrete label variables. In contrast to prior approaches such as convex relaxations, we propose an advantageous decoupling of the objective function into discrete and continuous subproblems and a novel, efficient optimization method related to ADMM. This approach preserves integrality of the discrete label variables and guarantees global convergence to a critical point. We demonstrate the advantages of our approach in several experiments including video object segmentation on the DAVIS data set and interactive image segmentation.

A Combinatorial Solution to Non-Rigid 3D Shape-to-Image Matching

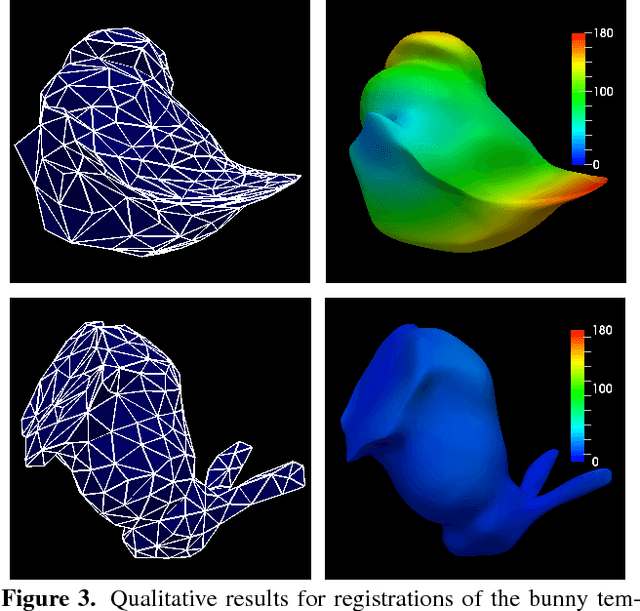
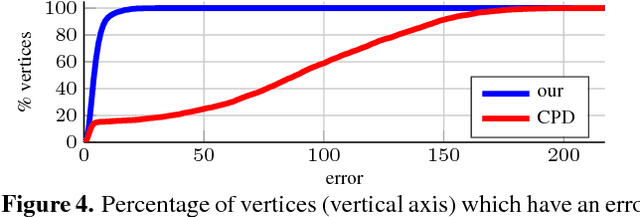
We propose a combinatorial solution for the problem of non-rigidly matching a 3D shape to 3D image data. To this end, we model the shape as a triangular mesh and allow each triangle of this mesh to be rigidly transformed to achieve a suitable matching to the image. By penalising the distance and the relative rotation between neighbouring triangles our matching compromises between image and shape information. In this paper, we resolve two major challenges: Firstly, we address the resulting large and NP-hard combinatorial problem with a suitable graph-theoretic approach. Secondly, we propose an efficient discretisation of the unbounded 6-dimensional Lie group SE(3). To our knowledge this is the first combinatorial formulation for non-rigid 3D shape-to-image matching. In contrast to existing local (gradient descent) optimisation methods, we obtain solutions that do not require a good initialisation and that are within a bound of the optimal solution. We evaluate the proposed method on the two problems of non-rigid 3D shape-to-shape and non-rigid 3D shape-to-image registration and demonstrate that it provides promising results.

Efficient Globally Optimal 2D-to-3D Deformable Shape Matching

We propose the first algorithm for non-rigid 2D-to-3D shape matching, where the input is a 2D shape represented as a planar curve and a 3D shape represented as a surface; the output is a continuous curve on the surface. We cast the problem as finding the shortest circular path on the prod- uct 3-manifold of the surface and the curve. We prove that the optimal matching can be computed in polynomial time with a (worst-case) complexity of $O(mn^2\log(n))$, where $m$ and $n$ denote the number of vertices on the template curve and the 3D shape respectively. We also demonstrate that in practice the runtime is essentially linear in $m\!\cdot\! n$ making it an efficient method for shape analysis and shape retrieval. Quantitative evaluation confirms that the method provides excellent results for sketch-based deformable 3D shape re- trieval.

An Experimental Comparison of Trust Region and Level Sets

High-order (non-linear) functionals have become very popular in segmentation, stereo and other computer vision problems. Level sets is a well established general gradient descent framework, which is directly applicable to optimization of such functionals and widely used in practice. Recently, another general optimization approach based on trust region methodology was proposed for regional non-linear functionals. Our goal is a comprehensive experimental comparison of these two frameworks in regard to practical efficiency, robustness to parameters, and optimality. We experiment on a wide range of problems with non-linear constraints on segment volume, appearance and shape.