Two-dimensional Decompositions of High-dimensional Configurations for Efficient Multi-vehicle Coordination at Intelligent Intersections

For multi-vehicle complex traffic scenarios in shared spaces such as intelligent intersections, safe coordination and trajectory planning is challenging due to computational complexity. To meet this challenge, we introduce a computationally efficient method for generating collision-free trajectories along predefined vehicle paths. We reformulate a constrained minimum-time trajectory planning problem as a problem in a high-dimensional configuration space, where conflict zones are modeled by high-dimensional polyhedra constructed from two-dimensional rectangles. Still, in such a formulation, as the number of vehicles involved increases, the computational complexity increases significantly. To address this, we propose two algorithms for near-optimal local optimization that significantly reduce the computational complexity by decomposing the high-dimensional problem into a sequence of 2D graph search problems. The resulting trajectories are then incorporated into a Nonlinear Model Predictive Control (NMPC) framework to ensure safe and smooth vehicle motion. We furthermore show in numerical evaluation that this approach significantly outperforms existing MILP-based time-scheduling; both in terms of objective-value and computational time.

How to Brake? Ethical Emergency Braking with Deep Reinforcement Learning

Connected and automated vehicles (CAVs) have the potential to enhance driving safety, for example by enabling safe vehicle following and more efficient traffic scheduling. For such future deployments, safety requirements should be addressed, where the primary such are avoidance of vehicle collisions and substantial mitigating of harm when collisions are unavoidable. However, conservative worst-case-based control strategies come at the price of reduced flexibility and may compromise overall performance. In light of this, we investigate how Deep Reinforcement Learning (DRL) can be leveraged to improve safety in multi-vehicle-following scenarios involving emergency braking. Specifically, we investigate how DRL with vehicle-to-vehicle communication can be used to ethically select an emergency breaking profile in scenarios where overall, or collective, three-vehicle harm reduction or collision avoidance shall be obtained instead of single-vehicle such. As an algorithm, we provide a hybrid approach that combines DRL with a previously published method based on analytical expressions for selecting optimal constant deceleration. By combining DRL with the previous method, the proposed hybrid approach increases the reliability compared to standalone DRL, while achieving superior performance in terms of overall harm reduction and collision avoidance.

Power Control of Multi-Layer Repeater Networks (POLARNet)

In this letter we introduce POLARNet -- power control of multi-layer repeater networks -- for local optimization of SNR given different repeater power constraints. We assume relays or repeaters in groups or layers spatially separated. Under ideal circumstances SISO narrow-band communication and TDD, the system may be viewed as a dual to a deep neural network, where activations, corresponding to repeater amplifications, are optimized and weight matrices, corresponding to channel matrices, are static. Repeater amplifications are locally optimized layer-by-layer in a forward-backward manner over compact sets. The method is applicable for a wide range of constraints on within-layer power/energy utilization, is furthermore gradient-free, step-size-free, and has proven monotonicity in the objective. Numerical simulations show significant improvement compared to upper bounds on the expected SNR. In addition, power distribution over multiple repeaters is shown to be superior to optimal selection of single repeaters in the layers.

Channel Orthogonalization with Reconfigurable Surfaces: General Models, Theoretical Limits, and Effective Configuration

We envision a future in which multi-antenna technology effectively exploits the spatial domain as a set of non-interfering orthogonal resources, allowing for flexible resource allocation and efficient modulation/demodulation. Reconfigurable intelligent surface (RIS) has emerged as a promising technology which allows shaping the propagation environment for improved performance. This paper studies the ability of three extended types of reconfigurable surface (RS), including the recently proposed beyond diagonal RIS (BD-RIS), to achieve perfectly orthogonal channels in a general multi-user multiple-input multiple-output (MU-MIMO) scenario. We propose practical implementations for the three types of RS consisting of passive components, and obtain the corresponding restrictions on their reconfigurability. We then use these restrictions to derive closed-form conditions for achieving arbitrary (orthogonal) channels. We also study the problem of optimal orthogonal channel selection for achieving high channel gain without active amplification at the RS, and we propose some methods with satisfying performance. Finally, we provide efficient channel estimation and RS configuration techniques such that all the computation, including the channel selection, may be performed at the base station (BS). The numerical results showcase the potential and practicality of RS channel orthogonalization, thus taking a step towards orthogonal spatial domain multiplexing (OSDM).

Hybrid Precoder Design for Angle-of-Departure Estimation with Limited-Resolution Phase Shifters

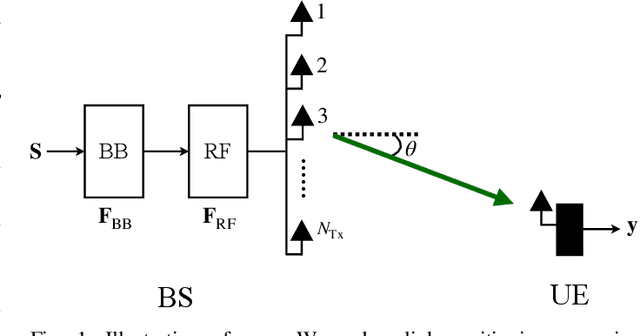
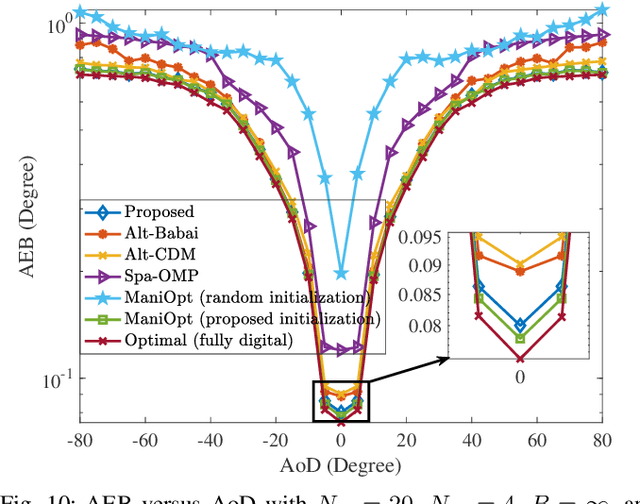
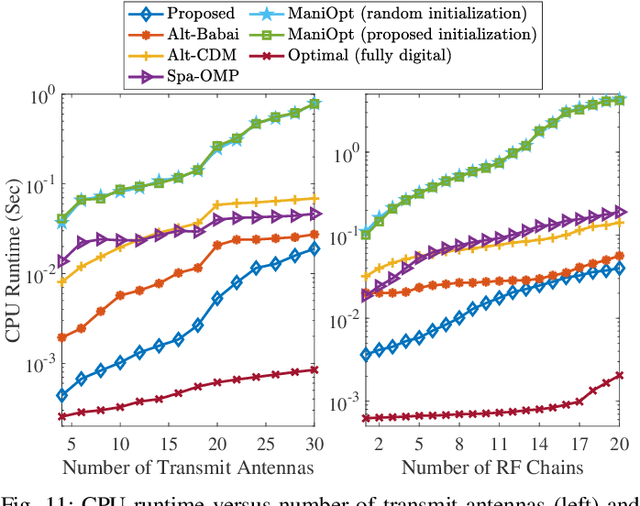
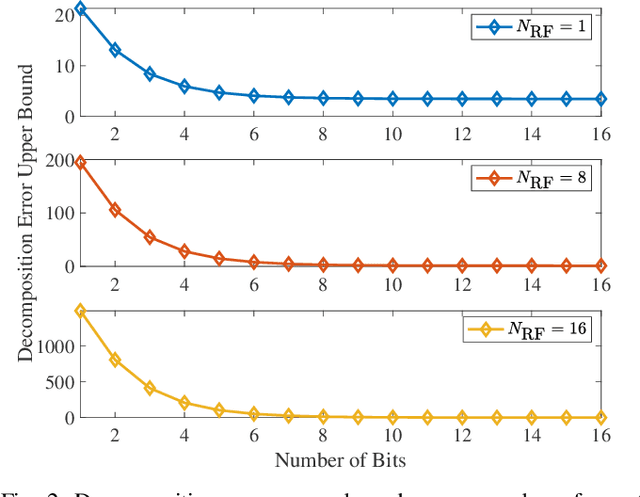
Hybrid analog-digital beamforming stands out as a key enabler for future communication systems with a massive number of antennas. In this paper, we investigate the hybrid precoder design problem for angle-of-departure (AoD) estimation, where we take into account the practical constraint on the limited resolution of phase shifters. Our goal is to design a radio-frequency (RF) precoder and a base-band (BB) precoder to estimate AoD of the user with a high accuracy. To this end, we propose a two-step strategy where we first obtain the fully digital precoder that minimizes the angle error bound, and then the resulting digital precoder is decomposed into an RF precoder and a BB precoder, based on the alternating optimization and the alternating direction method of multipliers. Besides, we derive the quantization error upper bound and analyse the convergence behavior of the proposed algorithm. Numerical results demonstrate the superior performance of the proposed method over state-of-the-art baselines.

Non-Negative Spherical Relaxations for Universe-Free Multi-Matching and Clustering

We propose a novel non-negative spherical relaxation for optimization problems over binary matrices with injectivity constraints, which in particular has applications in multi-matching and clustering. We relax respective binary matrix constraints to the (high-dimensional) non-negative sphere. To optimize our relaxed problem, we use a conditional power iteration method to iteratively improve the objective function, while at same time sweeping over a continuous scalar parameter that is (indirectly) related to the universe size (or number of clusters). Opposed to existing procedures that require to fix the integer universe size before optimization, our method automatically adjusts the analogous continuous parameter. Furthermore, while our approach shares similarities with spectral multi-matching and spectral clustering, our formulation has the strong advantage that we do not rely on additional post-processing procedures to obtain binary results. Our method shows compelling results in various multi-matching and clustering settings, even when compared to methods that use the ground truth universe size (or number of clusters).

Sparse Quadratic Optimisation over the Stiefel Manifold with Application to Permutation Synchronisation

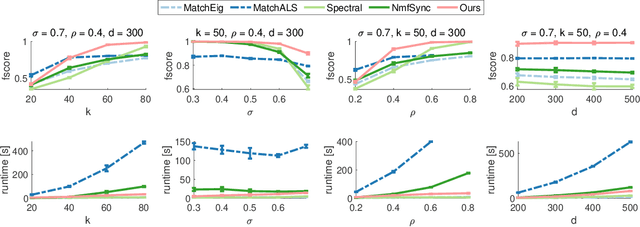
We address the non-convex optimisation problem of finding a sparse matrix on the Stiefel manifold (matrices with mutually orthogonal columns of unit length) that maximises (or minimises) a quadratic objective function. Optimisation problems on the Stiefel manifold occur for example in spectral relaxations of various combinatorial problems, such as graph matching, clustering, or permutation synchronisation. Although sparsity is a desirable property in such settings, it is mostly neglected in spectral formulations since existing solvers, e.g. based on eigenvalue decomposition, are unable to account for sparsity while at the same time maintaining global optimality guarantees. We fill this gap and propose a simple yet effective sparsity-promoting modification of the Orthogonal Iteration algorithm for finding the dominant eigenspace of a matrix. By doing so, we can guarantee that our method finds a Stiefel matrix that is globally optimal with respect to the quadratic objective function, while in addition being sparse. As a motivating application we consider the task of permutation synchronisation, which can be understood as a constrained clustering problem that has particular relevance for matching multiple images or 3D shapes in computer vision, computer graphics, and beyond. We demonstrate that the proposed approach outperforms previous methods in this domain.

Isometric Multi-Shape Matching

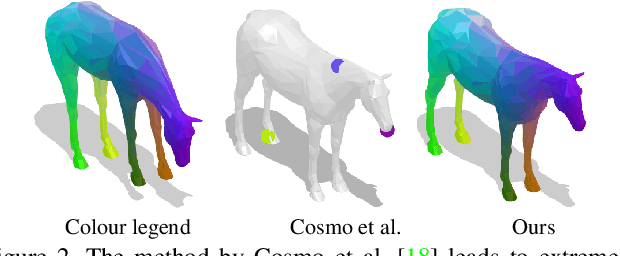
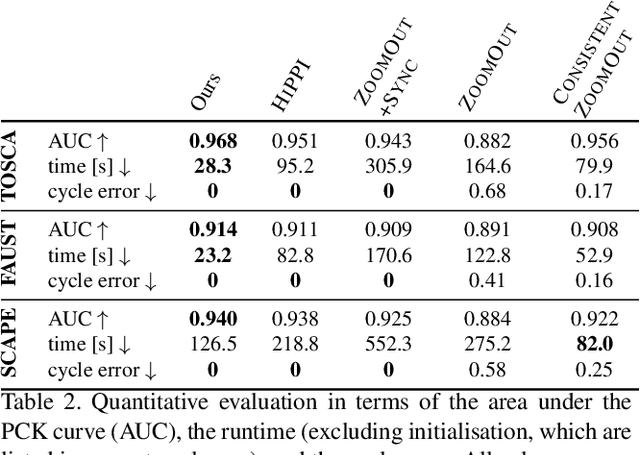
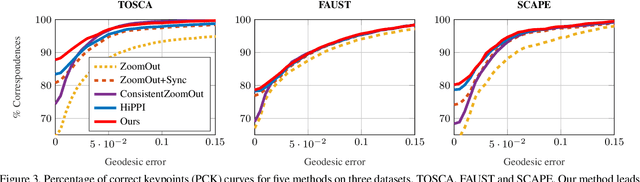
Finding correspondences between shapes is a fundamental problem in computer vision and graphics, which is relevant for many applications, including 3D reconstruction, object tracking, and style transfer. The vast majority of correspondence methods aim to find a solution between pairs of shapes, even if multiple instances of the same class are available. While isometries are often studied in shape correspondence problems, they have not been considered explicitly in the multi-matching setting. This paper closes this gap by proposing a novel optimisation formulation for isometric multi-shape matching. We present a suitable optimisation algorithm for solving our formulation and provide a convergence and complexity analysis. Our algorithm obtains multi-matchings that are by construction provably cycle-consistent. We demonstrate the superior performance of our method on various datasets and set the new state-of-the-art in isometric multi-shape matching.

Higher-order Projected Power Iterations for Scalable Multi-Matching

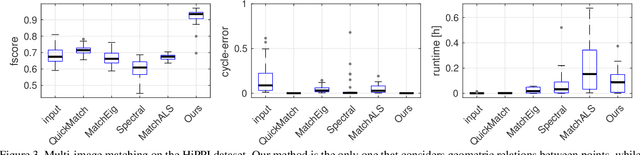
The matching of multiple objects (e.g. shapes or images) is a fundamental problem in vision and graphics. In order to robustly handle ambiguities, noise and repetitive patterns in challenging real-world settings, it is essential to take geometric consistency between points into account. Computationally, the multi-matching problem is difficult. It can be phrased as simultaneously solving multiple (NP-hard) quadratic assignment problems (QAPs) that are coupled via cycle-consistency constraints. The main limitations of existing multi-matching methods are that they either ignore geometric consistency and thus have limited robustness, or they are restricted to small-scale problems due to their (relatively) high computational cost. We address these shortcomings by introducing a Higher-order Projected Power Iteration method, which is (i) efficient and scales to tens of thousands of points, (ii) straightforward to implement, (iii) able to incorporate geometric consistency, and (iv) guarantees cycle-consistent multi-matchings. Experimentally we show that our approach is superior to existing methods.

Synchronisation of Partial Multi-Matchings via Non-negative Factorisations

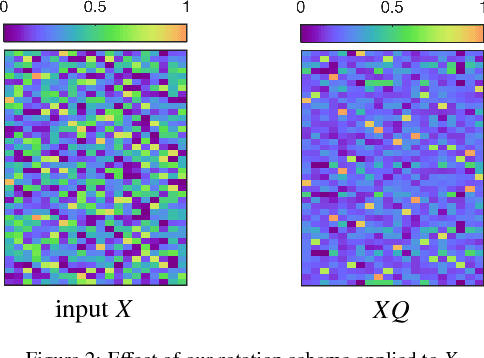
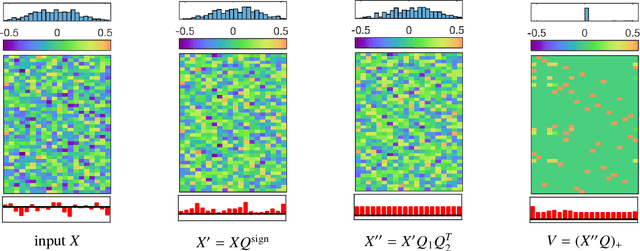
In this work we study permutation synchronisation for the challenging case of partial permutations, which plays an important role for the problem of matching multiple objects (e.g. images or shapes). The term synchronisation refers to the property that the set of pairwise matchings is cycle-consistent, i.e. in the full matching case all compositions of pairwise matchings over cycles must be equal to the identity. Motivated by clustering and matrix factorisation perspectives of cycle-consistency, we derive an algorithm to tackle the permutation synchronisation problem based on non-negative factorisations. In order to deal with the inherent non-convexity of the permutation synchronisation problem, we use an initialisation procedure based on a novel rotation scheme applied to the solution of the spectral relaxation. Moreover, this rotation scheme facilitates a convenient Euclidean projection to obtain a binary solution after solving our relaxed problem. In contrast to state-of-the-art methods, our approach is guaranteed to produce cycle-consistent results. We experimentally demonstrate the efficacy of our method and show that it achieves better results compared to existing methods.