Synchronisation of Partial Multi-Matchings via Non-negative Factorisations
Paper and Code
Jul 12, 2018
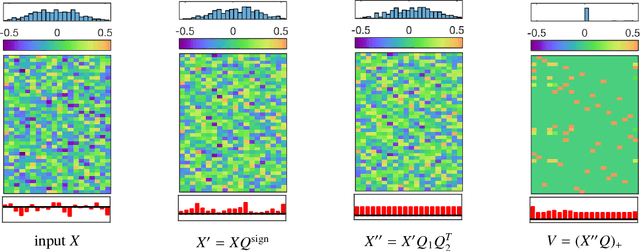
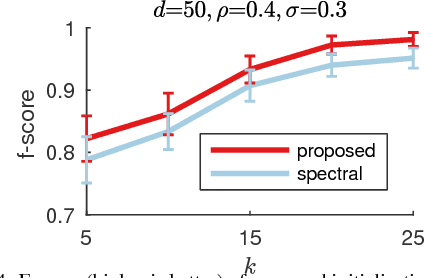
In this work we study permutation synchronisation for the challenging case of partial permutations, which plays an important role for the problem of matching multiple objects (e.g. images or shapes). The term synchronisation refers to the property that the set of pairwise matchings is cycle-consistent, i.e. in the full matching case all compositions of pairwise matchings over cycles must be equal to the identity. Motivated by clustering and matrix factorisation perspectives of cycle-consistency, we derive an algorithm to tackle the permutation synchronisation problem based on non-negative factorisations. In order to deal with the inherent non-convexity of the permutation synchronisation problem, we use an initialisation procedure based on a novel rotation scheme applied to the solution of the spectral relaxation. Moreover, this rotation scheme facilitates a convenient Euclidean projection to obtain a binary solution after solving our relaxed problem. In contrast to state-of-the-art methods, our approach is guaranteed to produce cycle-consistent results. We experimentally demonstrate the efficacy of our method and show that it achieves better results compared to existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge