Bayesian Inference of Stochastic Dynamical Networks

Network inference has been extensively studied in several fields, such as systems biology and social sciences. Learning network topology and internal dynamics is essential to understand mechanisms of complex systems. In particular, sparse topologies and stable dynamics are fundamental features of many real-world continuous-time networks. Given that usually only a partial set of nodes are able to observe, in this paper, we consider linear continuous-time systems to depict networks since they can model unmeasured nodes via transfer functions. Additionally, measurements tend to be noisy and with low and varying sampling frequencies. For this reason, we consider continuous-time models (CT) since discrete-time approximations often require fine-grained measurements and uniform sampling steps. The developed method applies dynamical structure functions (DSFs) derived from linear stochastic differential equations (SDEs) to describe networks of measured nodes. Further, a numerical sampling method, preconditioned Crank-Nicolson (pCN), is used to refine coarse-grained trajectories to improve inference accuracy. The simulation conducted on random and ring networks, and a synthetic biological network illustrate that our method achieves state-of-the-art performance compared with group sparse Bayesian learning (GSBL), BINGO, kernel-based methods, dynGENIE3, GENIE3 and ARNI. In particular, these are challenging networks, suggesting that the developed method can be applied under a wide range of contexts.

DBSegment: Fast and robust segmentation of deep brain structures -- Evaluation of transportability across acquisition domains

Segmenting deep brain structures from magnetic resonance images is important for patient diagnosis, surgical planning, and research. Most current state-of-the-art solutions follow a segmentation-by-registration approach, where subject MRIs are mapped to a template with well-defined segmentations. However, registration-based pipelines are time-consuming, thus, limiting their clinical use. This paper uses deep learning to provide a robust and efficient deep brain segmentation solution. The method consists of a pre-processing step to conform all MRI images to the same orientation, followed by a convolutional neural network using the nnU-Net framework. We use a total of 14 datasets from both research and clinical collections. Of these, seven were used for training and validation and seven were retained for independent testing. We trained the network to segment 30 deep brain structures, as well as a brain mask, using labels generated from a registration-based approach. We evaluated the generalizability of the network by performing a leave-one-dataset-out cross-validation, and extensive testing on external datasets. Furthermore, we assessed cross-domain transportability by evaluating the results separately on different domains. We achieved an average DSC of 0.89 $\pm$ 0.04 on the independent testing datasets when compared to the registration-based gold standard. On our test system, the computation time decreased from 42 minutes for a reference registration-based pipeline to 1 minute. Our proposed method is fast, robust, and generalizes with high reliability. It can be extended to the segmentation of other brain structures. The method is publicly available on GitHub, as well as a pip package for convenient usage.

Machine Discovery of Partial Differential Equations from Spatiotemporal Data

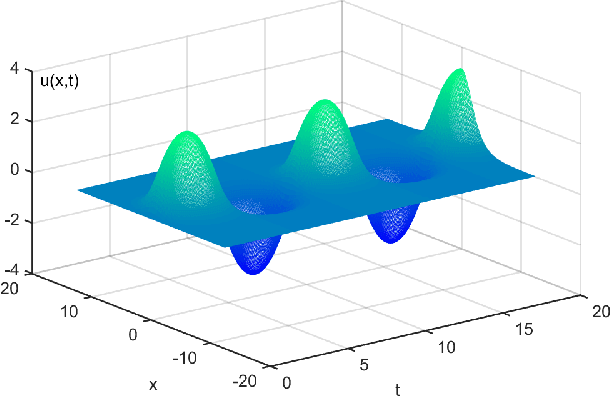
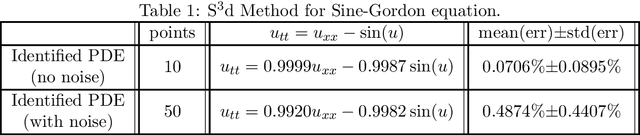
The study presents a general framework for discovering underlying Partial Differential Equations (PDEs) using measured spatiotemporal data. The method, called Sparse Spatiotemporal System Discovery ($\text{S}^3\text{d}$), decides which physical terms are necessary and which can be removed (because they are physically negligible in the sense that they do not affect the dynamics too much) from a pool of candidate functions. The method is built on the recent development of Sparse Bayesian Learning; which enforces the sparsity in the to-be-identified PDEs, and therefore can balance the model complexity and fitting error with theoretical guarantees. Without leveraging prior knowledge or assumptions in the discovery process, we use an automated approach to discover ten types of PDEs, including the famous Navier-Stokes and sine-Gordon equations, from simulation data alone. Moreover, we demonstrate our data-driven discovery process with the Complex Ginzburg-Landau Equation (CGLE) using data measured from a traveling-wave convection experiment. Our machine discovery approach presents solutions that has the potential to inspire, support and assist physicists for the establishment of physical laws from measured spatiotemporal data, especially in notorious fields that are often too complex to allow a straightforward establishment of physical law, such as biophysics, fluid dynamics, neuroscience or nonlinear optics.

Data-driven Discovery of Cyber-Physical Systems

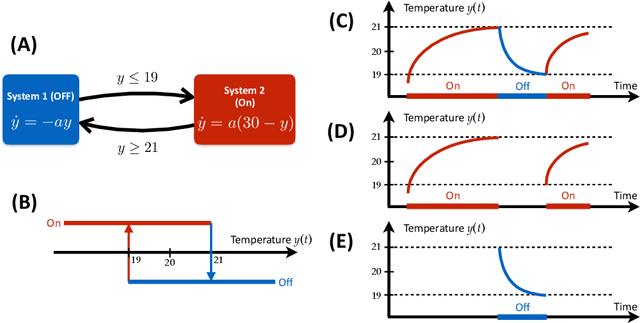
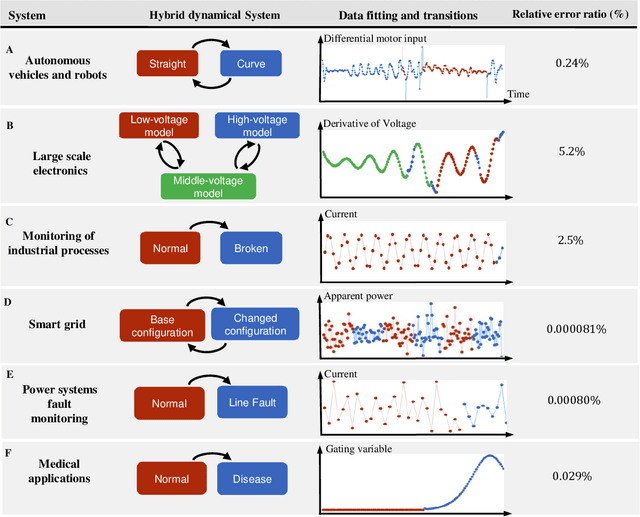
Cyber-physical systems (CPSs) embed software into the physical world. They appear in a wide range of applications such as smart grids, robotics, intelligent manufacture and medical monitoring. CPSs have proved resistant to modeling due to their intrinsic complexity arising from the combination of physical components and cyber components and the interaction between them. This study proposes a general framework for reverse engineering CPSs directly from data. The method involves the identification of physical systems as well as the inference of transition logic. It has been applied successfully to a number of real-world examples ranging from mechanical and electrical systems to medical applications. The novel framework seeks to enable researchers to make predictions concerning the trajectory of CPSs based on the discovered model. Such information has been proven essential for the assessment of the performance of CPS, the design of failure-proof CPS and the creation of design guidelines for new CPSs.

Synchronisation of Partial Multi-Matchings via Non-negative Factorisations

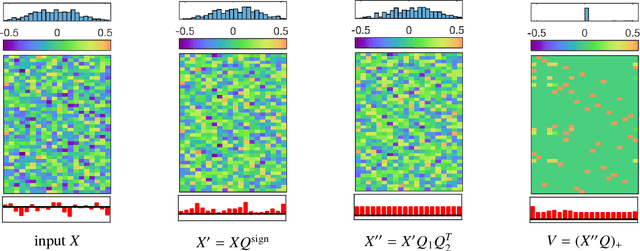
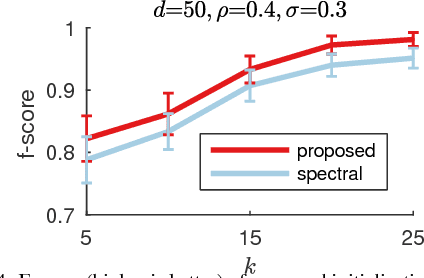
In this work we study permutation synchronisation for the challenging case of partial permutations, which plays an important role for the problem of matching multiple objects (e.g. images or shapes). The term synchronisation refers to the property that the set of pairwise matchings is cycle-consistent, i.e. in the full matching case all compositions of pairwise matchings over cycles must be equal to the identity. Motivated by clustering and matrix factorisation perspectives of cycle-consistency, we derive an algorithm to tackle the permutation synchronisation problem based on non-negative factorisations. In order to deal with the inherent non-convexity of the permutation synchronisation problem, we use an initialisation procedure based on a novel rotation scheme applied to the solution of the spectral relaxation. Moreover, this rotation scheme facilitates a convenient Euclidean projection to obtain a binary solution after solving our relaxed problem. In contrast to state-of-the-art methods, our approach is guaranteed to produce cycle-consistent results. We experimentally demonstrate the efficacy of our method and show that it achieves better results compared to existing methods.

Distributed methods for synchronization of orthogonal matrices over graphs

This paper addresses the problem of synchronizing orthogonal matrices over directed graphs. For synchronized transformations (or matrices), composite transformations over loops equal the identity. We formulate the synchronization problem as a least-squares optimization problem with nonlinear constraints. The synchronization problem appears as one of the key components in applications ranging from 3D-localization to image registration. The main contributions of this work can be summarized as the introduction of two novel algorithms; one for symmetric graphs and one for graphs that are possibly asymmetric. Under general conditions, the former has guaranteed convergence to the solution of a spectral relaxation to the synchronization problem. The latter is stable for small step sizes when the graph is quasi-strongly connected. The proposed methods are verified in numerical simulations.

Shape-aware Surface Reconstruction from Sparse 3D Point-Clouds

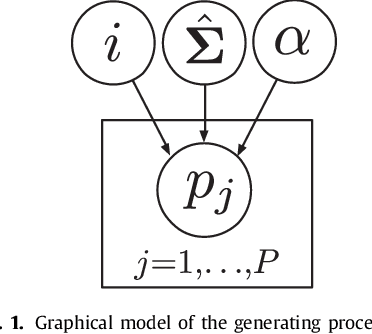
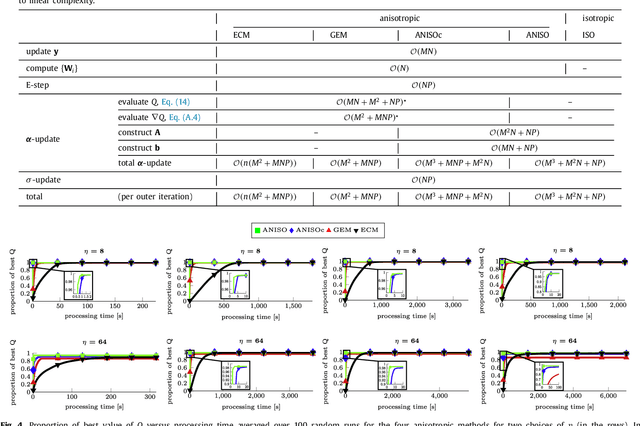
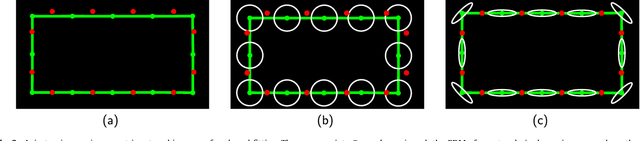
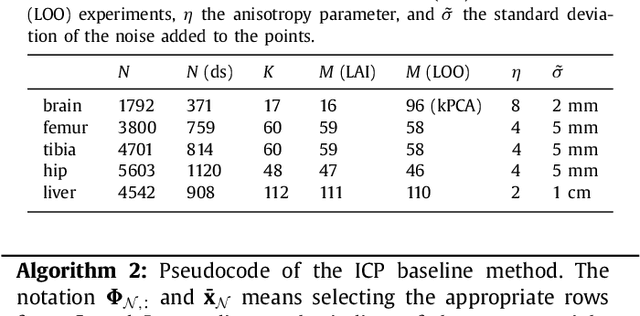
The reconstruction of an object's shape or surface from a set of 3D points plays an important role in medical image analysis, e.g. in anatomy reconstruction from tomographic measurements or in the process of aligning intra-operative navigation and preoperative planning data. In such scenarios, one usually has to deal with sparse data, which significantly aggravates the problem of reconstruction. However, medical applications often provide contextual information about the 3D point data that allow to incorporate prior knowledge about the shape that is to be reconstructed. To this end, we propose the use of a statistical shape model (SSM) as a prior for surface reconstruction. The SSM is represented by a point distribution model (PDM), which is associated with a surface mesh. Using the shape distribution that is modelled by the PDM, we formulate the problem of surface reconstruction from a probabilistic perspective based on a Gaussian Mixture Model (GMM). In order to do so, the given points are interpreted as samples of the GMM. By using mixture components with anisotropic covariances that are "oriented" according to the surface normals at the PDM points, a surface-based fitting is accomplished. Estimating the parameters of the GMM in a maximum a posteriori manner yields the reconstruction of the surface from the given data points. We compare our method to the extensively used Iterative Closest Points method on several different anatomical datasets/SSMs (brain, femur, tibia, hip, liver) and demonstrate superior accuracy and robustness on sparse data.

Linear Shape Deformation Models with Local Support Using Graph-based Structured Matrix Factorisation

Representing 3D shape deformations by linear models in high-dimensional space has many applications in computer vision and medical imaging, such as shape-based interpolation or segmentation. Commonly, using Principal Components Analysis a low-dimensional (affine) subspace of the high-dimensional shape space is determined. However, the resulting factors (the most dominant eigenvectors of the covariance matrix) have global support, i.e. changing the coefficient of a single factor deforms the entire shape. In this paper, a method to obtain deformation factors with local support is presented. The benefits of such models include better flexibility and interpretability as well as the possibility of interactively deforming shapes locally. For that, based on a well-grounded theoretical motivation, we formulate a matrix factorisation problem employing sparsity and graph-based regularisation terms. We demonstrate that for brain shapes our method outperforms the state of the art in local support models with respect to generalisation ability and sparse shape reconstruction, whereas for human body shapes our method gives more realistic deformations.

On Transitive Consistency for Linear Invertible Transformations between Euclidean Coordinate Systems

Transitive consistency is an intrinsic property for collections of linear invertible transformations between Euclidean coordinate frames. In practice, when the transformations are estimated from data, this property is lacking. This work addresses the problem of synchronizing transformations that are not transitively consistent. Once the transformations have been synchronized, they satisfy the transitive consistency condition - a transformation from frame $A$ to frame $C$ is equal to the composite transformation of first transforming A to B and then transforming B to C. The coordinate frames correspond to nodes in a graph and the transformations correspond to edges in the same graph. Two direct or centralized synchronization methods are presented for different graph topologies; the first one for quasi-strongly connected graphs, and the second one for connected graphs. As an extension of the second method, an iterative Gauss-Newton method is presented, which is later adapted to the case of affine and Euclidean transformations. Two distributed synchronization methods are also presented for orthogonal matrices, which can be seen as distributed versions of the two direct or centralized methods; they are similar in nature to standard consensus protocols used for distributed averaging. When the transformations are orthogonal matrices, a bound on the optimality gap can be computed. Simulations show that the gap is almost right, even for noise large in magnitude. This work also contributes on a theoretical level by providing linear algebraic relationships for transitively consistent transformations. One of the benefits of the proposed methods is their simplicity - basic linear algebraic methods are used, e.g., the Singular Value Decomposition (SVD). For a wide range of parameter settings, the methods are numerically validated.

A Solution for Multi-Alignment by Transformation Synchronisation

The alignment of a set of objects by means of transformations plays an important role in computer vision. Whilst the case for only two objects can be solved globally, when multiple objects are considered usually iterative methods are used. In practice the iterative methods perform well if the relative transformations between any pair of objects are free of noise. However, if only noisy relative transformations are available (e.g. due to missing data or wrong correspondences) the iterative methods may fail. Based on the observation that the underlying noise-free transformations can be retrieved from the null space of a matrix that can directly be obtained from pairwise alignments, this paper presents a novel method for the synchronisation of pairwise transformations such that they are transitively consistent. Simulations demonstrate that for noisy transformations, a large proportion of missing data and even for wrong correspondence assignments the method delivers encouraging results.