Machine Discovery of Partial Differential Equations from Spatiotemporal Data

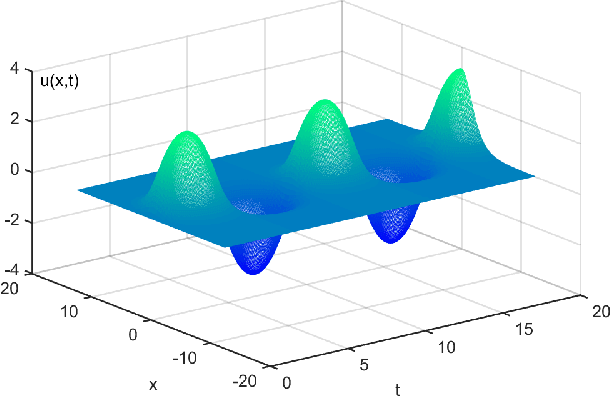
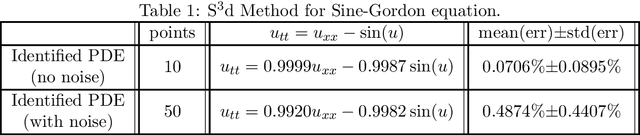
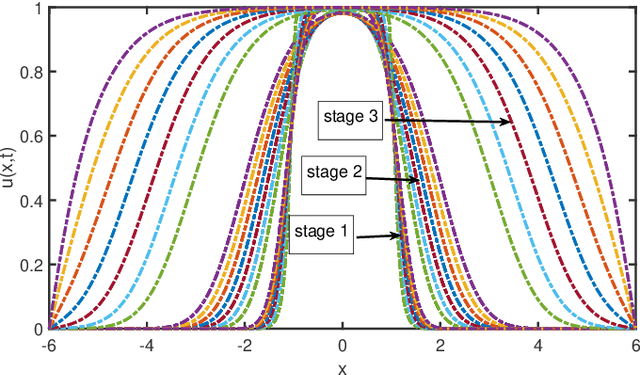
The study presents a general framework for discovering underlying Partial Differential Equations (PDEs) using measured spatiotemporal data. The method, called Sparse Spatiotemporal System Discovery ($\text{S}^3\text{d}$), decides which physical terms are necessary and which can be removed (because they are physically negligible in the sense that they do not affect the dynamics too much) from a pool of candidate functions. The method is built on the recent development of Sparse Bayesian Learning; which enforces the sparsity in the to-be-identified PDEs, and therefore can balance the model complexity and fitting error with theoretical guarantees. Without leveraging prior knowledge or assumptions in the discovery process, we use an automated approach to discover ten types of PDEs, including the famous Navier-Stokes and sine-Gordon equations, from simulation data alone. Moreover, we demonstrate our data-driven discovery process with the Complex Ginzburg-Landau Equation (CGLE) using data measured from a traveling-wave convection experiment. Our machine discovery approach presents solutions that has the potential to inspire, support and assist physicists for the establishment of physical laws from measured spatiotemporal data, especially in notorious fields that are often too complex to allow a straightforward establishment of physical law, such as biophysics, fluid dynamics, neuroscience or nonlinear optics.

Data-driven Discovery of Cyber-Physical Systems

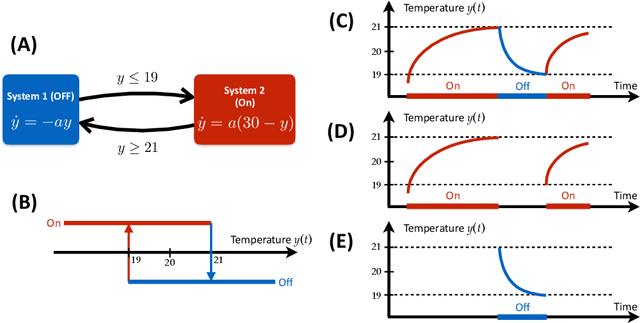
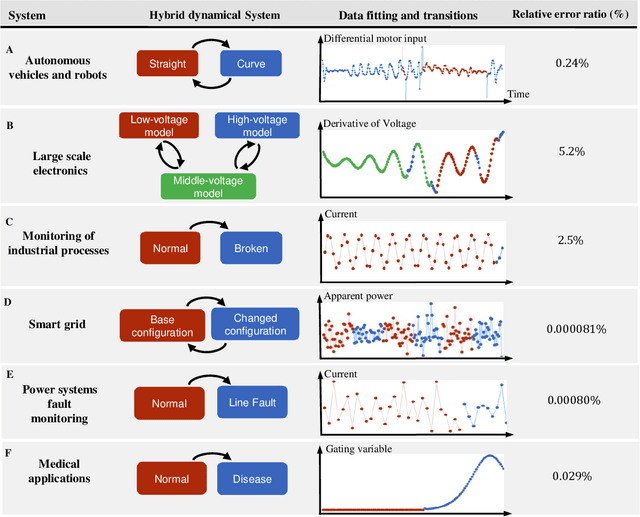
Cyber-physical systems (CPSs) embed software into the physical world. They appear in a wide range of applications such as smart grids, robotics, intelligent manufacture and medical monitoring. CPSs have proved resistant to modeling due to their intrinsic complexity arising from the combination of physical components and cyber components and the interaction between them. This study proposes a general framework for reverse engineering CPSs directly from data. The method involves the identification of physical systems as well as the inference of transition logic. It has been applied successfully to a number of real-world examples ranging from mechanical and electrical systems to medical applications. The novel framework seeks to enable researchers to make predictions concerning the trajectory of CPSs based on the discovered model. Such information has been proven essential for the assessment of the performance of CPS, the design of failure-proof CPS and the creation of design guidelines for new CPSs.