Exploring Adult Glioma through MRI: A Review of Publicly Available Datasets to Guide Efficient Image Analysis

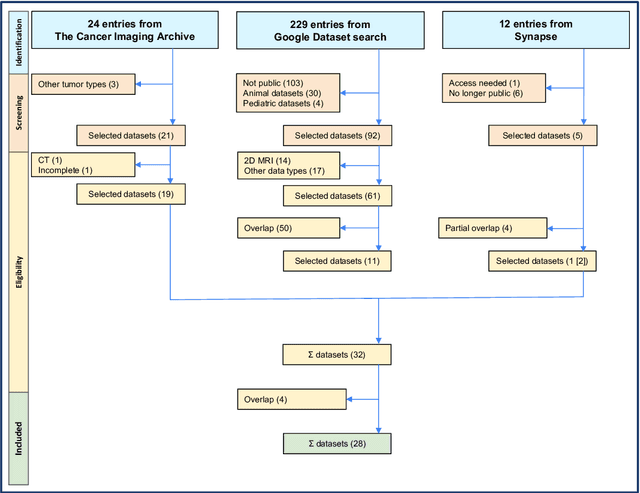
Publicly available data is essential for the progress of medical image analysis, in particular for crafting machine learning models. Glioma is the most common group of primary brain tumors, and magnetic resonance imaging (MRI) is a widely used modality in their diagnosis and treatment. However, the availability and quality of public datasets for glioma MRI are not well known. In this review, we searched for public datasets for glioma MRI using Google Dataset Search, The Cancer Imaging Archive (TCIA), and Synapse. A total of 28 datasets published between 2005 and May 2024 were found, containing 62019 images from 5515 patients. We analyzed the characteristics of these datasets, such as the origin, size, format, annotation, and accessibility. Additionally, we examined the distribution of tumor types, grades, and stages among the datasets. The implications of the evolution of the WHO classification on tumors of the brain are discussed, in particular the 2021 update that significantly changed the definition of glioblastoma. Additionally, potential research questions that could be explored using these datasets were highlighted, such as tumor evolution through malignant transformation, MRI normalization, and tumor segmentation. Interestingly, only two datasets among the 28 studied reflect the current WHO classification. This review provides a comprehensive overview of the publicly available datasets for glioma MRI currently at our disposal, providing aid to medical image analysis researchers in their decision-making on efficient dataset choice.

DBSegment: Fast and robust segmentation of deep brain structures -- Evaluation of transportability across acquisition domains

Segmenting deep brain structures from magnetic resonance images is important for patient diagnosis, surgical planning, and research. Most current state-of-the-art solutions follow a segmentation-by-registration approach, where subject MRIs are mapped to a template with well-defined segmentations. However, registration-based pipelines are time-consuming, thus, limiting their clinical use. This paper uses deep learning to provide a robust and efficient deep brain segmentation solution. The method consists of a pre-processing step to conform all MRI images to the same orientation, followed by a convolutional neural network using the nnU-Net framework. We use a total of 14 datasets from both research and clinical collections. Of these, seven were used for training and validation and seven were retained for independent testing. We trained the network to segment 30 deep brain structures, as well as a brain mask, using labels generated from a registration-based approach. We evaluated the generalizability of the network by performing a leave-one-dataset-out cross-validation, and extensive testing on external datasets. Furthermore, we assessed cross-domain transportability by evaluating the results separately on different domains. We achieved an average DSC of 0.89 $\pm$ 0.04 on the independent testing datasets when compared to the registration-based gold standard. On our test system, the computation time decreased from 42 minutes for a reference registration-based pipeline to 1 minute. Our proposed method is fast, robust, and generalizes with high reliability. It can be extended to the segmentation of other brain structures. The method is publicly available on GitHub, as well as a pip package for convenient usage.

Shape-aware Surface Reconstruction from Sparse 3D Point-Clouds

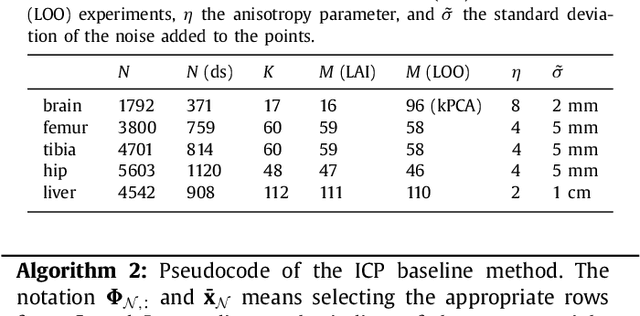
The reconstruction of an object's shape or surface from a set of 3D points plays an important role in medical image analysis, e.g. in anatomy reconstruction from tomographic measurements or in the process of aligning intra-operative navigation and preoperative planning data. In such scenarios, one usually has to deal with sparse data, which significantly aggravates the problem of reconstruction. However, medical applications often provide contextual information about the 3D point data that allow to incorporate prior knowledge about the shape that is to be reconstructed. To this end, we propose the use of a statistical shape model (SSM) as a prior for surface reconstruction. The SSM is represented by a point distribution model (PDM), which is associated with a surface mesh. Using the shape distribution that is modelled by the PDM, we formulate the problem of surface reconstruction from a probabilistic perspective based on a Gaussian Mixture Model (GMM). In order to do so, the given points are interpreted as samples of the GMM. By using mixture components with anisotropic covariances that are "oriented" according to the surface normals at the PDM points, a surface-based fitting is accomplished. Estimating the parameters of the GMM in a maximum a posteriori manner yields the reconstruction of the surface from the given data points. We compare our method to the extensively used Iterative Closest Points method on several different anatomical datasets/SSMs (brain, femur, tibia, hip, liver) and demonstrate superior accuracy and robustness on sparse data.

Linear Shape Deformation Models with Local Support Using Graph-based Structured Matrix Factorisation

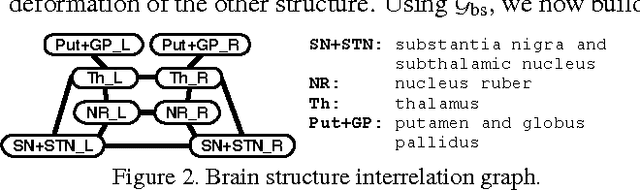
Representing 3D shape deformations by linear models in high-dimensional space has many applications in computer vision and medical imaging, such as shape-based interpolation or segmentation. Commonly, using Principal Components Analysis a low-dimensional (affine) subspace of the high-dimensional shape space is determined. However, the resulting factors (the most dominant eigenvectors of the covariance matrix) have global support, i.e. changing the coefficient of a single factor deforms the entire shape. In this paper, a method to obtain deformation factors with local support is presented. The benefits of such models include better flexibility and interpretability as well as the possibility of interactively deforming shapes locally. For that, based on a well-grounded theoretical motivation, we formulate a matrix factorisation problem employing sparsity and graph-based regularisation terms. We demonstrate that for brain shapes our method outperforms the state of the art in local support models with respect to generalisation ability and sparse shape reconstruction, whereas for human body shapes our method gives more realistic deformations.

A Solution for Multi-Alignment by Transformation Synchronisation

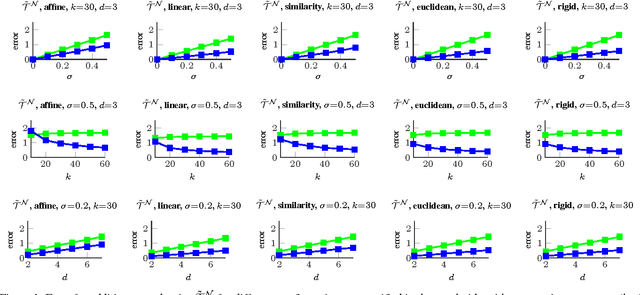
The alignment of a set of objects by means of transformations plays an important role in computer vision. Whilst the case for only two objects can be solved globally, when multiple objects are considered usually iterative methods are used. In practice the iterative methods perform well if the relative transformations between any pair of objects are free of noise. However, if only noisy relative transformations are available (e.g. due to missing data or wrong correspondences) the iterative methods may fail. Based on the observation that the underlying noise-free transformations can be retrieved from the null space of a matrix that can directly be obtained from pairwise alignments, this paper presents a novel method for the synchronisation of pairwise transformations such that they are transitively consistent. Simulations demonstrate that for noisy transformations, a large proportion of missing data and even for wrong correspondence assignments the method delivers encouraging results.