Exploring Adult Glioma through MRI: A Review of Publicly Available Datasets to Guide Efficient Image Analysis

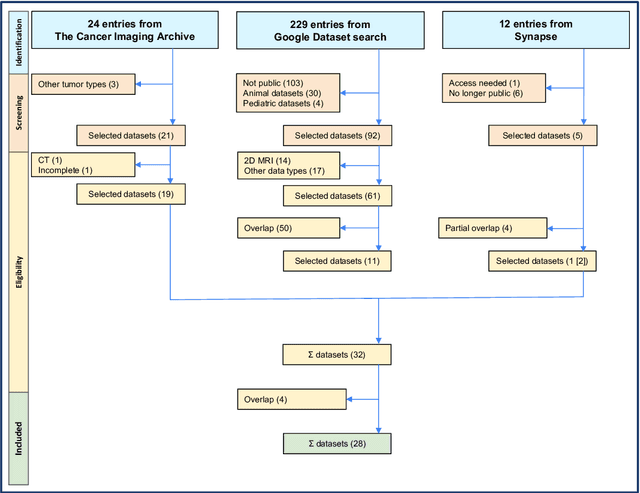
Publicly available data is essential for the progress of medical image analysis, in particular for crafting machine learning models. Glioma is the most common group of primary brain tumors, and magnetic resonance imaging (MRI) is a widely used modality in their diagnosis and treatment. However, the availability and quality of public datasets for glioma MRI are not well known. In this review, we searched for public datasets for glioma MRI using Google Dataset Search, The Cancer Imaging Archive (TCIA), and Synapse. A total of 28 datasets published between 2005 and May 2024 were found, containing 62019 images from 5515 patients. We analyzed the characteristics of these datasets, such as the origin, size, format, annotation, and accessibility. Additionally, we examined the distribution of tumor types, grades, and stages among the datasets. The implications of the evolution of the WHO classification on tumors of the brain are discussed, in particular the 2021 update that significantly changed the definition of glioblastoma. Additionally, potential research questions that could be explored using these datasets were highlighted, such as tumor evolution through malignant transformation, MRI normalization, and tumor segmentation. Interestingly, only two datasets among the 28 studied reflect the current WHO classification. This review provides a comprehensive overview of the publicly available datasets for glioma MRI currently at our disposal, providing aid to medical image analysis researchers in their decision-making on efficient dataset choice.

Identifiability of Differential-Algebraic Systems

Data-driven modeling of dynamical systems often faces numerous data-related challenges. A fundamental requirement is the existence of a unique set of parameters for a chosen model structure, an issue commonly referred to as identifiability. Although this problem is well studied for ordinary differential equations (ODEs), few studies have focused on the more general class of systems described by differential-algebraic equations (DAEs). Examples of DAEs include dynamical systems with algebraic equations representing conservation laws or approximating fast dynamics. This work introduces a novel identifiability test for models characterized by nonlinear DAEs. Unlike previous approaches, our test only requires prior knowledge of the system equations and does not need nonlinear transformation, index reduction, or numerical integration of the DAEs. We employed our identifiability analysis across a diverse range of DAE models, illustrating how system identifiability depends on the choices of sensors, experimental conditions, and model structures. Given the added challenges involved in identifying DAEs when compared to ODEs, we anticipate that our findings will have broad applicability and contribute significantly to the development and validation of data-driven methods for DAEs and other structure-preserving models.