Adaptive Certified Training: Towards Better Accuracy-Robustness Tradeoffs

As deep learning models continue to advance and are increasingly utilized in real-world systems, the issue of robustness remains a major challenge. Existing certified training methods produce models that achieve high provable robustness guarantees at certain perturbation levels. However, the main problem of such models is a dramatically low standard accuracy, i.e. accuracy on clean unperturbed data, that makes them impractical. In this work, we consider a more realistic perspective of maximizing the robustness of a model at certain levels of (high) standard accuracy. To this end, we propose a novel certified training method based on a key insight that training with adaptive certified radii helps to improve both the accuracy and robustness of the model, advancing state-of-the-art accuracy-robustness tradeoffs. We demonstrate the effectiveness of the proposed method on MNIST, CIFAR-10, and TinyImageNet datasets. Particularly, on CIFAR-10 and TinyImageNet, our method yields models with up to two times higher robustness, measured as an average certified radius of a test set, at the same levels of standard accuracy compared to baseline approaches.

Universe Points Representation Learning for Partial Multi-Graph Matching

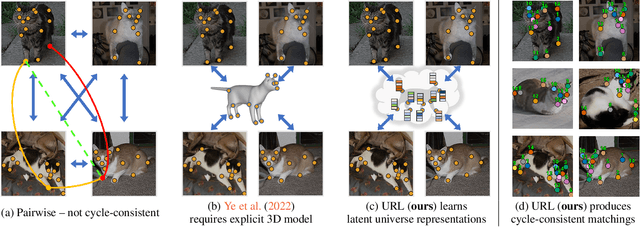
Many challenges from natural world can be formulated as a graph matching problem. Previous deep learning-based methods mainly consider a full two-graph matching setting. In this work, we study the more general partial matching problem with multi-graph cycle consistency guarantees. Building on a recent progress in deep learning on graphs, we propose a novel data-driven method (URL) for partial multi-graph matching, which uses an object-to-universe formulation and learns latent representations of abstract universe points. The proposed approach advances the state of the art in semantic keypoint matching problem, evaluated on Pascal VOC, CUB, and Willow datasets. Moreover, the set of controlled experiments on a synthetic graph matching dataset demonstrates the scalability of our method to graphs with large number of nodes and its robustness to high partiality.

Efficient and Flexible Sublabel-Accurate Energy Minimization

We address the problem of minimizing a class of energy functions consisting of data and smoothness terms that commonly occur in machine learning, computer vision, and pattern recognition. While discrete optimization methods are able to give theoretical optimality guarantees, they can only handle a finite number of labels and therefore suffer from label discretization bias. Existing continuous optimization methods can find sublabel-accurate solutions, but they are not efficient for large label spaces. In this work, we propose an efficient sublabel-accurate method that utilizes the best properties of both continuous and discrete models. We separate the problem into two sequential steps: (i) global discrete optimization for selecting the label range, and (ii) efficient continuous sublabel-accurate local refinement of a convex approximation of the energy function in the chosen range. Doing so allows us to achieve a boost in time and memory efficiency while practically keeping the accuracy at the same level as continuous convex relaxation methods, and in addition, providing theoretical optimality guarantees at the level of discrete methods. Finally, we show the flexibility of the proposed approach to general pairwise smoothness terms, so that it is applicable to a wide range of regularizations. Experiments on the illustrating example of the image denoising problem demonstrate the properties of the proposed method. The code reproducing experiments is available at \url{https://github.com/nurlanov-zh/sublabel-accurate-alpha-expansion}.