A Polyhedral Study of Lifted Multicuts

Fundamental to many applications in data analysis are the decompositions of a graph, i.e. partitions of the node set into component-inducing subsets. One way of encoding decompositions is by multicuts, the subsets of those edges that straddle distinct components. Recently, a lifting of multicuts from a graph $G = (V, E)$ to an augmented graph $\hat G = (V, E \cup F)$ has been proposed in the field of image analysis, with the goal of obtaining a more expressive characterization of graph decompositions in which it is made explicit also for pairs $F \subseteq \tbinom{V}{2} \setminus E$ of non-neighboring nodes whether these are in the same or distinct components. In this work, we study in detail the polytope in $\mathbb{R}^{E \cup F}$ whose vertices are precisely the characteristic vectors of multicuts of $\hat G$ lifted from $G$, connecting it, in particular, to the rich body of prior work on the clique partitioning and multilinear polytope.

Discrete-Continuous ADMM for Transductive Inference in Higher-Order MRFs

This paper introduces a novel algorithm for transductive inference in higher-order MRFs, where the unary energies are parameterized by a variable classifier. The considered task is posed as a joint optimization problem in the continuous classifier parameters and the discrete label variables. In contrast to prior approaches such as convex relaxations, we propose an advantageous decoupling of the objective function into discrete and continuous subproblems and a novel, efficient optimization method related to ADMM. This approach preserves integrality of the discrete label variables and guarantees global convergence to a critical point. We demonstrate the advantages of our approach in several experiments including video object segmentation on the DAVIS data set and interactive image segmentation.

Efficient Algorithms for Moral Lineage Tracing

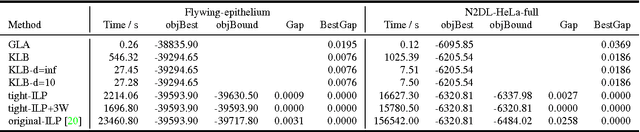
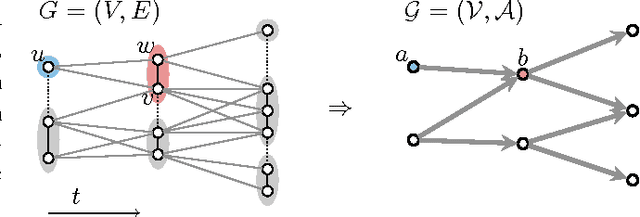
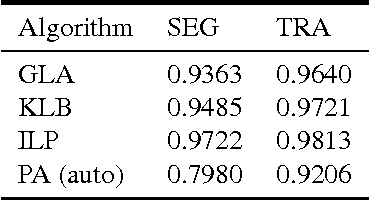
Lineage tracing, the joint segmentation and tracking of living cells as they move and divide in a sequence of light microscopy images, is a challenging task. Jug et al. have proposed a mathematical abstraction of this task, the moral lineage tracing problem (MLTP), whose feasible solutions define both a segmentation of every image and a lineage forest of cells. Their branch-and-cut algorithm, however, is prone to many cuts and slow convergence for large instances. To address this problem, we make three contributions: (i) we devise the first efficient primal feasible local search algorithms for the MLTP, (ii) we improve the branch-and-cut algorithm by separating tighter cutting planes and by incorporating our primal algorithms, (iii) we show in experiments that our algorithms find accurate solutions on the problem instances of Jug et al. and scale to larger instances, leveraging moral lineage tracing to practical significance.