Efficient Algorithms for Moral Lineage Tracing
Paper and Code
Aug 25, 2017
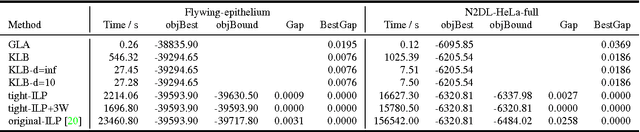
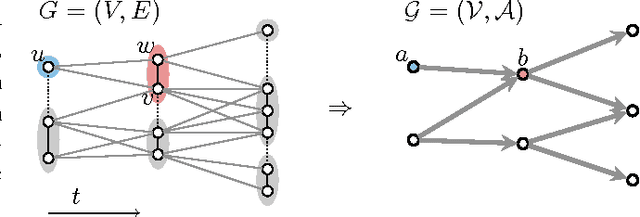
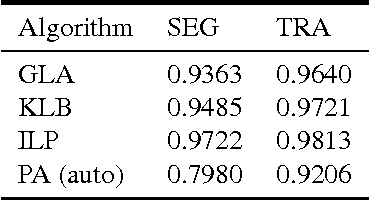
Lineage tracing, the joint segmentation and tracking of living cells as they move and divide in a sequence of light microscopy images, is a challenging task. Jug et al. have proposed a mathematical abstraction of this task, the moral lineage tracing problem (MLTP), whose feasible solutions define both a segmentation of every image and a lineage forest of cells. Their branch-and-cut algorithm, however, is prone to many cuts and slow convergence for large instances. To address this problem, we make three contributions: (i) we devise the first efficient primal feasible local search algorithms for the MLTP, (ii) we improve the branch-and-cut algorithm by separating tighter cutting planes and by incorporating our primal algorithms, (iii) we show in experiments that our algorithms find accurate solutions on the problem instances of Jug et al. and scale to larger instances, leveraging moral lineage tracing to practical significance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge