Stationary Velocity Fields on Matrix Groups for Deformable Image Registration

The stationary velocity field (SVF) approach allows to build parametrizations of invertible deformation fields, which is often a desirable property in image registration. Its expressiveness is particularly attractive when used as a block following a machine learning-inspired network. However, it can struggle with large deformations. We extend the SVF approach to matrix groups, in particular $\SE(3)$. This moves Euclidean transformations into the low-frequency part, towards which network architectures are often naturally biased, so that larger motions can be recovered more easily. This requires an extension of the flow equation, for which we provide sufficient conditions for existence. We further prove a decomposition condition that allows us to apply a scaling-and-squaring approach for efficient numerical integration of the flow equation. We numerically validate the approach on inter-patient registration of 3D MRI images of the human brain.

On the Connection between Dynamical Optimal Transport and Functional Lifting

Functional lifting methods provide a tool for approximating solutions of difficult non-convex problems by embedding them into a larger space. In this work, we investigate a mathematically rigorous formulation based on embedding into the space of pointwise probability measures over a fixed range $\Gamma$. Interestingly, this approach can be derived as a generalization of the theory of dynamical optimal transport. Imposing the established continuity equation as a constraint corresponds to variational models with first-order regularization. By modifying the continuity equation, the approach can also be extended to models with higher-order regularization.

Deformable Groupwise Image Registration using Low-Rank and Sparse Decomposition

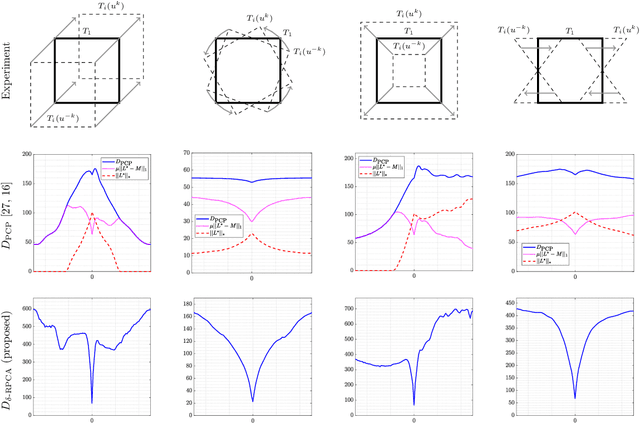
Low-rank and sparse decompositions and robust PCA (RPCA) are highly successful techniques in image processing and have recently found use in groupwise image registration. In this paper, we investigate the drawbacks of the most common RPCA-dissimi\-larity metric in image registration and derive an improved version. In particular, this new metric models low-rank requirements through explicit constraints instead of penalties and thus avoids the pitfalls of the established metric. Equipped with total variation regularization, we present a theoretically justified multilevel scheme based on first-order primal-dual optimization to solve the resulting non-parametric registration problem. As confirmed by numerical experiments, our metric especially lends itself to data involving recurring changes in object appearance and potential sparse perturbations. We numerically compare its peformance to a number of related approaches.

Fully-deformable 3D image registration in two seconds

We present a highly parallel method for accurate and efficient variational deformable 3D image registration on a consumer-grade graphics processing unit (GPU). We build on recent matrix-free variational approaches and specialize the concepts to the massively-parallel manycore architecture provided by the GPU. Compared to a parallel and optimized CPU implementation, this allows us to achieve an average speedup of 32.53 on 986 real-world CT thorax-abdomen follow-up scans. At a resolution of approximately $256^3$ voxels, the average runtime is 1.99 seconds for the full registration. On the publicly available DIR-lab benchmark, our method ranks third with respect to average landmark error at an average runtime of 0.32 seconds.

A multi-contrast MRI approach to thalamus segmentation

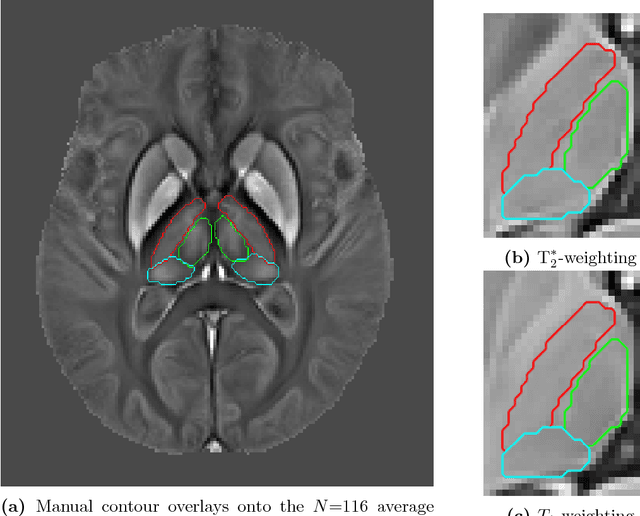
Thalamic alterations are relevant to many neurological disorders including Alzheimer's disease, Parkinson's disease and multiple sclerosis. Routine interventions to improve symptom severity in movement disorders, for example, often consist of surgery or deep brain stimulation to diencephalic nuclei. Therefore, accurate delineation of grey matter thalamic subregions is of the upmost clinical importance. MRI is highly appropriate for structural segmentation as it provides different views of the anatomy from a single scanning session. Though with several contrasts potentially available, it is also of increasing importance to develop new image segmentation techniques that can operate multi-spectrally. We hereby propose a new segmentation method for use with multi-modality data, which we evaluated for automated segmentation of major thalamic subnuclear groups using T1-, T2*-weighted and quantitative susceptibility mapping (QSM) information. The proposed method consists of four steps: highly iterative image co-registration, manual segmentation on the average training-data template, supervised learning for pattern recognition, and a final convex optimisation step imposing further spatial constraints to refine the solution. This led to solutions in greater agreement with manual segmentation than the standard Morel atlas based approach. Furthermore, we show that the multi-contrast approach boosts segmentation performances. We then investigated whether prior knowledge using the training-template contours could further improve convex segmentation accuracy and robustness, which led to highly precise multi-contrast segmentations in single subjects. This approach can be extended to most 3D imaging data types and any region of interest discernible in single scans or multi-subject templates.

A matrix-free approach to parallel and memory-efficient deformable image registration

We present a novel computational approach to fast and memory-efficient deformable image registration. In the variational registration model, the computation of the objective function derivatives is the computationally most expensive operation, both in terms of runtime and memory requirements. In order to target this bottleneck, we analyze the matrix structure of gradient and Hessian computations for the case of the normalized gradient fields distance measure and curvature regularization. Based on this analysis, we derive equivalent matrix-free closed-form expressions for derivative computations, eliminating the need for storing intermediate results and the costs of sparse matrix arithmetic. This has further benefits: (1) matrix computations can be fully parallelized, (2) memory complexity for derivative computation is reduced from linear to constant, and (3) overall computation times are substantially reduced. In comparison with an optimized matrix-based reference implementation, the CPU implementation achieves speedup factors between 3.1 and 9.7, and we are able to handle substantially higher resolutions. Using a GPU implementation, we achieve an additional speedup factor of up to 9.2. Furthermore, we evaluated the approach on real-world medical datasets. On ten publicly available lung CT images from the DIR-Lab 4DCT dataset, we achieve the best mean landmark error of 0.93 mm compared to other submissions on the DIR-Lab website, with an average runtime of only 9.23 s. Complete non-rigid registration of full-size 3D thorax-abdomen CT volumes from oncological follow-up is achieved in 12.6 s. The experimental results show that the proposed matrix-free algorithm enables the use of variational registration models also in applications which were previously impractical due to memory or runtime restrictions.

Image reconstruction with imperfect forward models and applications in deblurring

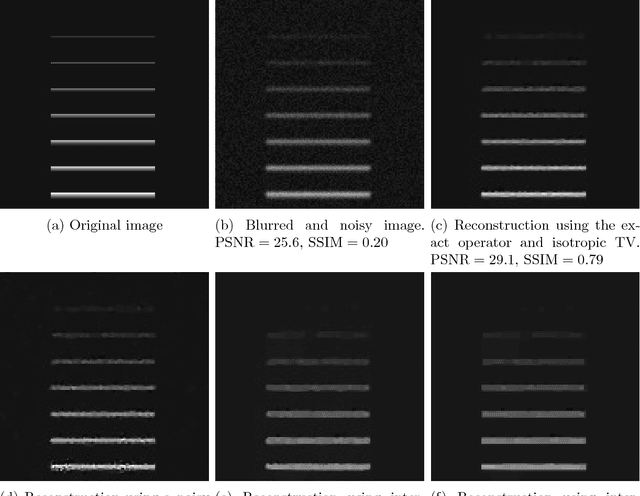
We present and analyse an approach to image reconstruction problems with imperfect forward models based on partially ordered spaces - Banach lattices. In this approach, errors in the data and in the forward models are described using order intervals. The method can be characterised as the lattice analogue of the residual method, where the feasible set is defined by linear inequality constraints. The study of this feasible set is the main contribution of this paper. Convexity of this feasible set is examined in several settings and modifications for introducing additional information about the forward operator are considered. Numerical examples demonstrate the performance of the method in deblurring with errors in the blurring kernel.

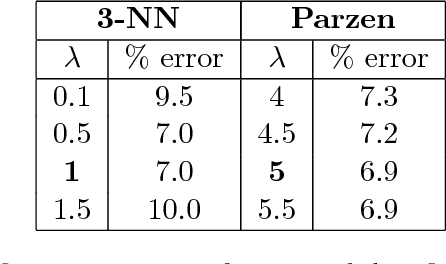
A graph cut approach to 3D tree delineation, using integrated airborne LiDAR and hyperspectral imagery

Recognising individual trees within remotely sensed imagery has important applications in forest ecology and management. Several algorithms for tree delineation have been suggested, mostly based on locating local maxima or inverted basins in raster canopy height models (CHMs) derived from Light Detection And Ranging (LiDAR) data or photographs. However, these algorithms often lead to inaccurate estimates of forest stand characteristics due to the limited information content of raster CHMs. Here we develop a 3D tree delineation method which uses graph cut to delineate trees from the full 3D LiDAR point cloud, and also makes use of any optical imagery available (hyperspectral imagery in our case). First, conventional methods are used to locate local maxima in the CHM and generate an initial map of trees. Second, a graph is built from the LiDAR point cloud, fused with the hyperspectral data. For computational efficiency, the feature space of hyperspectral imagery is reduced using robust PCA. Third, a multi-class normalised cut is applied to the graph, using the initial map of trees to constrain the number of clusters and their locations. Finally, recursive normalised cut is used to subdivide, if necessary, each of the clusters identified by the initial analysis. We call this approach Multiclass Cut followed by Recursive Cut (MCRC). The effectiveness of MCRC was tested using three datasets: i) NewFor, ii) a coniferous forest in the Italian Alps, and iii) a deciduous woodland in the UK. The performance of MCRC was usually superior to that of other delineation methods, and was further improved by including high-resolution optical imagery. Since MCRC delineates the entire LiDAR point cloud in 3D, it allows individual crown characteristics to be measured. By making full use of the data available, graph cut has the potential to considerably improve the accuracy of tree delineation.

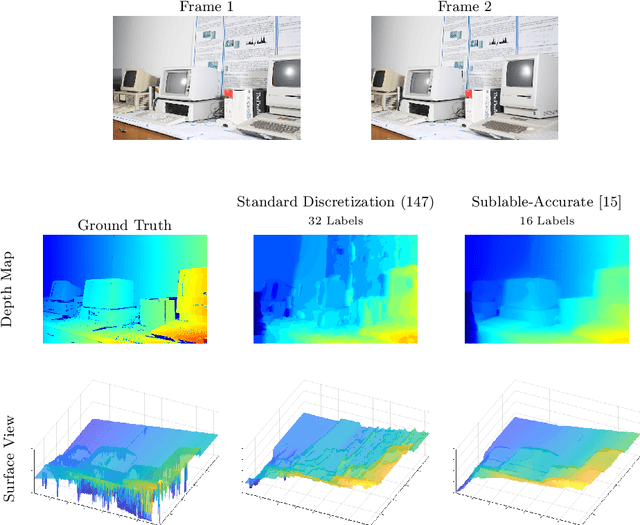
Sublabel-Accurate Convex Relaxation of Vectorial Multilabel Energies

Convex relaxations of nonconvex multilabel problems have been demonstrated to produce superior (provably optimal or near-optimal) solutions to a variety of classical computer vision problems. Yet, they are of limited practical use as they require a fine discretization of the label space, entailing a huge demand in memory and runtime. In this work, we propose the first sublabel accurate convex relaxation for vectorial multilabel problems. The key idea is that we approximate the dataterm of the vectorial labeling problem in a piecewise convex (rather than piecewise linear) manner. As a result we have a more faithful approximation of the original cost function that provides a meaningful interpretation for the fractional solutions of the relaxed convex problem. In numerous experiments on large-displacement optical flow estimation and on color image denoising we demonstrate that the computed solutions have superior quality while requiring much lower memory and runtime.

Sublabel-Accurate Relaxation of Nonconvex Energies

We propose a novel spatially continuous framework for convex relaxations based on functional lifting. Our method can be interpreted as a sublabel-accurate solution to multilabel problems. We show that previously proposed functional lifting methods optimize an energy which is linear between two labels and hence require (often infinitely) many labels for a faithful approximation. In contrast, the proposed formulation is based on a piecewise convex approximation and therefore needs far fewer labels. In comparison to recent MRF-based approaches, our method is formulated in a spatially continuous setting and shows less grid bias. Moreover, in a local sense, our formulation is the tightest possible convex relaxation. It is easy to implement and allows an efficient primal-dual optimization on GPUs. We show the effectiveness of our approach on several computer vision problems.