On the Connection between Dynamical Optimal Transport and Functional Lifting

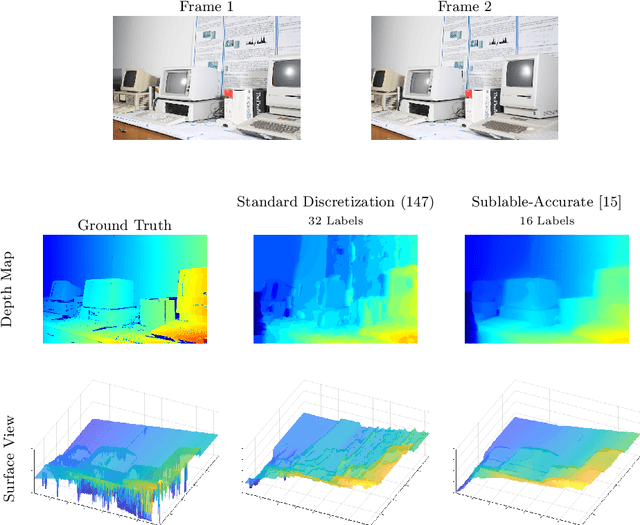
Functional lifting methods provide a tool for approximating solutions of difficult non-convex problems by embedding them into a larger space. In this work, we investigate a mathematically rigorous formulation based on embedding into the space of pointwise probability measures over a fixed range $\Gamma$. Interestingly, this approach can be derived as a generalization of the theory of dynamical optimal transport. Imposing the established continuity equation as a constraint corresponds to variational models with first-order regularization. By modifying the continuity equation, the approach can also be extended to models with higher-order regularization.

Optimized imaging using non-rigid registration

The extraordinary improvements of modern imaging devices offer access to data with unprecedented information content. However, widely used image processing methodologies fall far short of exploiting the full breadth of information offered by numerous types of scanning probe, optical, and electron microscopies. In many applications, it is necessary to keep measurement intensities below a desired threshold. We propose a methodology for extracting an increased level of information by processing a series of data sets suffering, in particular, from high degree of spatial uncertainty caused by complex multiscale motion during the acquisition process. An important role is played by a nonrigid pixel-wise registration method that can cope with low signal-to-noise ratios. This is accompanied by formulating objective quality measures which replace human intervention and visual inspection in the processing chain. Scanning transmission electron microscopy of siliceous zeolite material exhibits the above-mentioned obstructions and therefore serves as orientation and a test of our procedures.