Introduction to Regularization and Learning Methods for Inverse Problems

These lecture notes evolve around mathematical concepts arising in inverse problems. We start by introducing inverse problems through examples such as differentiation, deconvolution, computed tomography and phase retrieval. This then leads us to the framework of well-posedness and first considerations regarding reconstruction and inversion approaches. The second chapter then first deals with classical regularization theory of inverse problems in Hilbert spaces. After introducing the pseudo-inverse, we review the concept of convergent regularization. Within this chapter we then proceed to ask the question of how to realize practical reconstruction algorithms. Here, we mainly focus on Tikhonov and sparsity promoting regularization in finite dimensional spaces. In the third chapter, we dive into modern deep-learning methods, which allow solving inverse problems in a data-dependent approach. The intersection between inverse problems and machine learning is a rapidly growing field and our exposition here restricts itself to a very limited selection of topics. Among them are learned regularization, fully-learned Bayesian estimation, post-processing strategies and plug-n-play methods.

On the Connection between Dynamical Optimal Transport and Functional Lifting

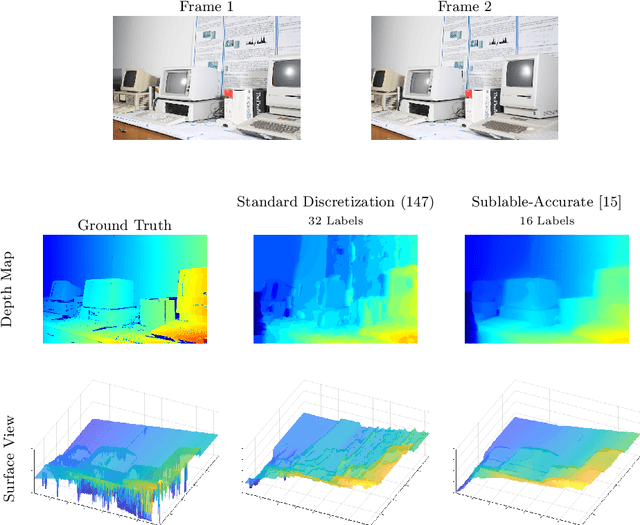
Functional lifting methods provide a tool for approximating solutions of difficult non-convex problems by embedding them into a larger space. In this work, we investigate a mathematically rigorous formulation based on embedding into the space of pointwise probability measures over a fixed range $\Gamma$. Interestingly, this approach can be derived as a generalization of the theory of dynamical optimal transport. Imposing the established continuity equation as a constraint corresponds to variational models with first-order regularization. By modifying the continuity equation, the approach can also be extended to models with higher-order regularization.