Deformable Groupwise Image Registration using Low-Rank and Sparse Decomposition
Paper and Code
Jan 10, 2020

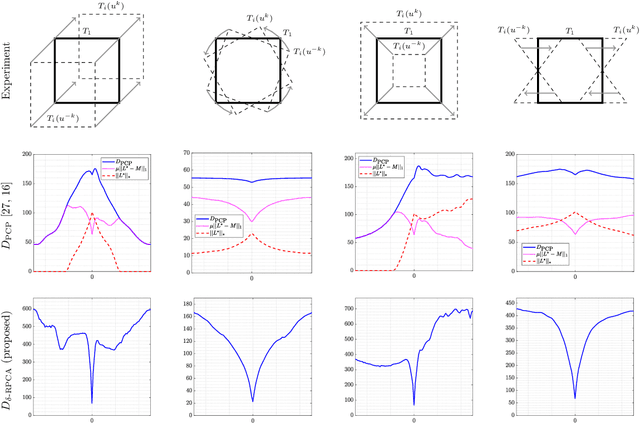

Low-rank and sparse decompositions and robust PCA (RPCA) are highly successful techniques in image processing and have recently found use in groupwise image registration. In this paper, we investigate the drawbacks of the most common RPCA-dissimi\-larity metric in image registration and derive an improved version. In particular, this new metric models low-rank requirements through explicit constraints instead of penalties and thus avoids the pitfalls of the established metric. Equipped with total variation regularization, we present a theoretically justified multilevel scheme based on first-order primal-dual optimization to solve the resulting non-parametric registration problem. As confirmed by numerical experiments, our metric especially lends itself to data involving recurring changes in object appearance and potential sparse perturbations. We numerically compare its peformance to a number of related approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge