Image reconstruction with imperfect forward models and applications in deblurring
Paper and Code
Oct 23, 2017
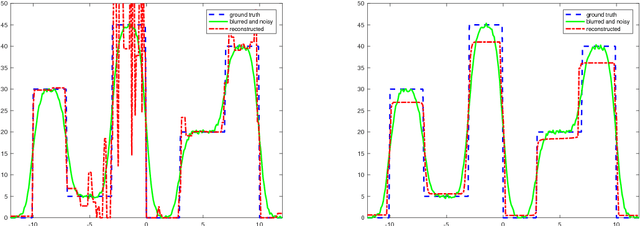

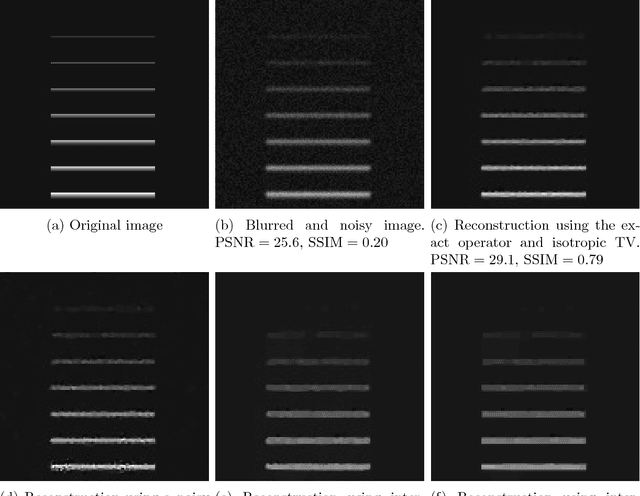
We present and analyse an approach to image reconstruction problems with imperfect forward models based on partially ordered spaces - Banach lattices. In this approach, errors in the data and in the forward models are described using order intervals. The method can be characterised as the lattice analogue of the residual method, where the feasible set is defined by linear inequality constraints. The study of this feasible set is the main contribution of this paper. Convexity of this feasible set is examined in several settings and modifications for introducing additional information about the forward operator are considered. Numerical examples demonstrate the performance of the method in deblurring with errors in the blurring kernel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge