Adversarial Transferability in Deep Denoising Models: Theoretical Insights and Robustness Enhancement via Out-of-Distribution Typical Set Sampling

Deep learning-based image denoising models demonstrate remarkable performance, but their lack of robustness analysis remains a significant concern. A major issue is that these models are susceptible to adversarial attacks, where small, carefully crafted perturbations to input data can cause them to fail. Surprisingly, perturbations specifically crafted for one model can easily transfer across various models, including CNNs, Transformers, unfolding models, and plug-and-play models, leading to failures in those models as well. Such high adversarial transferability is not observed in classification models. We analyze the possible underlying reasons behind the high adversarial transferability through a series of hypotheses and validation experiments. By characterizing the manifolds of Gaussian noise and adversarial perturbations using the concept of typical set and the asymptotic equipartition property, we prove that adversarial samples deviate slightly from the typical set of the original input distribution, causing the models to fail. Based on these insights, we propose a novel adversarial defense method: the Out-of-Distribution Typical Set Sampling Training strategy (TS). TS not only significantly enhances the model's robustness but also marginally improves denoising performance compared to the original model.

A Tunable Despeckling Neural Network Stabilized via Diffusion Equation

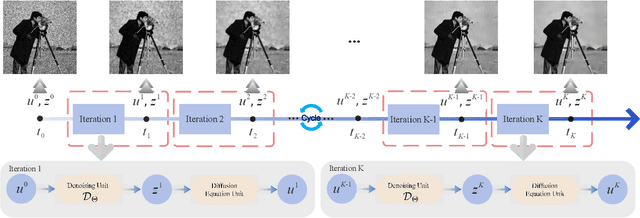
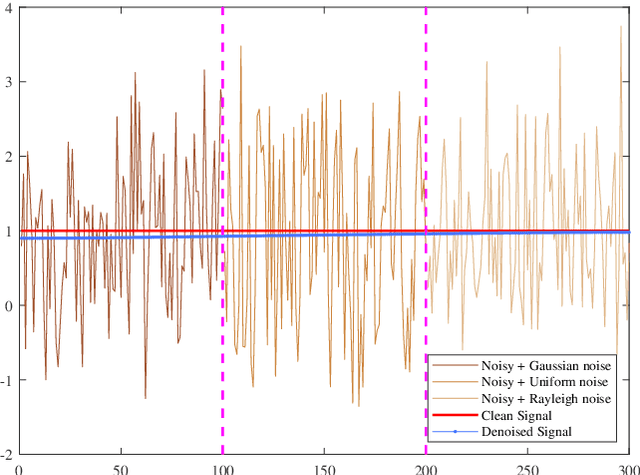
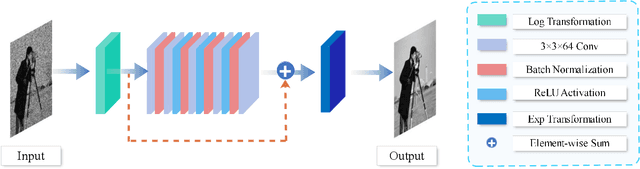
Multiplicative Gamma noise remove is a critical research area in the application of synthetic aperture radar (SAR) imaging, where neural networks serve as a potent tool. However, real-world data often diverges from theoretical models, exhibiting various disturbances, which makes the neural network less effective. Adversarial attacks work by finding perturbations that significantly disrupt functionality of neural networks, as the inherent instability of neural networks makes them highly susceptible. A network designed to withstand such extreme cases can more effectively mitigate general disturbances in real SAR data. In this work, the dissipative nature of diffusion equations is employed to underpin a novel approach for countering adversarial attacks and improve the resistance of real noise disturbance. We propose a tunable, regularized neural network that unrolls a denoising unit and a regularization unit into a single network for end-to-end training. In the network, the denoising unit and the regularization unit are composed of the denoising network and the simplest linear diffusion equation respectively. The regularization unit enhances network stability, allowing post-training time step adjustments to effectively mitigate the adverse impacts of adversarial attacks. The stability and convergence of our model are theoretically proven, and in the experiments, we compare our model with several state-of-the-art denoising methods on simulated images, adversarial samples, and real SAR images, yielding superior results in both quantitative and visual evaluations.

Adversarial Training for Physics-Informed Neural Networks

Physics-informed neural networks have shown great promise in solving partial differential equations. However, due to insufficient robustness, vanilla PINNs often face challenges when solving complex PDEs, especially those involving multi-scale behaviors or solutions with sharp or oscillatory characteristics. To address these issues, based on the projected gradient descent adversarial attack, we proposed an adversarial training strategy for PINNs termed by AT-PINNs. AT-PINNs enhance the robustness of PINNs by fine-tuning the model with adversarial samples, which can accurately identify model failure locations and drive the model to focus on those regions during training. AT-PINNs can also perform inference with temporal causality by selecting the initial collocation points around temporal initial values. We implement AT-PINNs to the elliptic equation with multi-scale coefficients, Poisson equation with multi-peak solutions, Burgers equation with sharp solutions and the Allen-Cahn equation. The results demonstrate that AT-PINNs can effectively locate and reduce failure regions. Moreover, AT-PINNs are suitable for solving complex PDEs, since locating failure regions through adversarial attacks is independent of the size of failure regions or the complexity of the distribution.