A Tunable Despeckling Neural Network Stabilized via Diffusion Equation

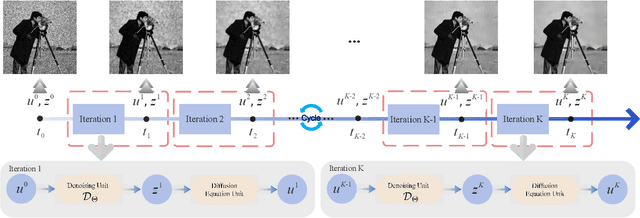
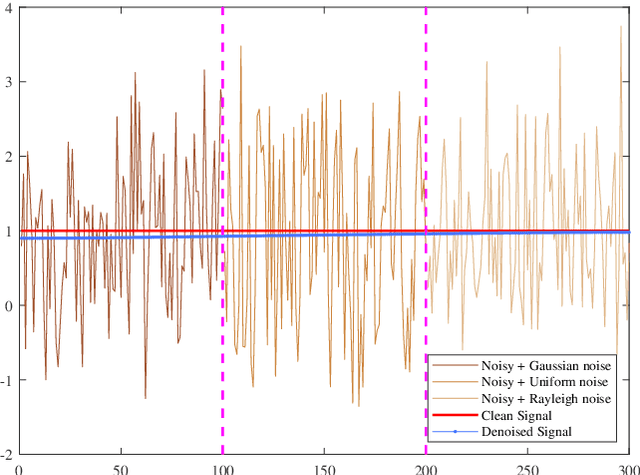
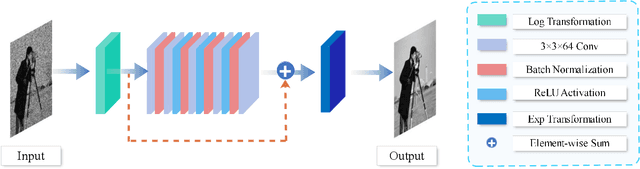
Multiplicative Gamma noise remove is a critical research area in the application of synthetic aperture radar (SAR) imaging, where neural networks serve as a potent tool. However, real-world data often diverges from theoretical models, exhibiting various disturbances, which makes the neural network less effective. Adversarial attacks work by finding perturbations that significantly disrupt functionality of neural networks, as the inherent instability of neural networks makes them highly susceptible. A network designed to withstand such extreme cases can more effectively mitigate general disturbances in real SAR data. In this work, the dissipative nature of diffusion equations is employed to underpin a novel approach for countering adversarial attacks and improve the resistance of real noise disturbance. We propose a tunable, regularized neural network that unrolls a denoising unit and a regularization unit into a single network for end-to-end training. In the network, the denoising unit and the regularization unit are composed of the denoising network and the simplest linear diffusion equation respectively. The regularization unit enhances network stability, allowing post-training time step adjustments to effectively mitigate the adverse impacts of adversarial attacks. The stability and convergence of our model are theoretically proven, and in the experiments, we compare our model with several state-of-the-art denoising methods on simulated images, adversarial samples, and real SAR images, yielding superior results in both quantitative and visual evaluations.