Rachel Morris
Uniform Convergence of Adversarially Robust Classifiers
Jun 20, 2024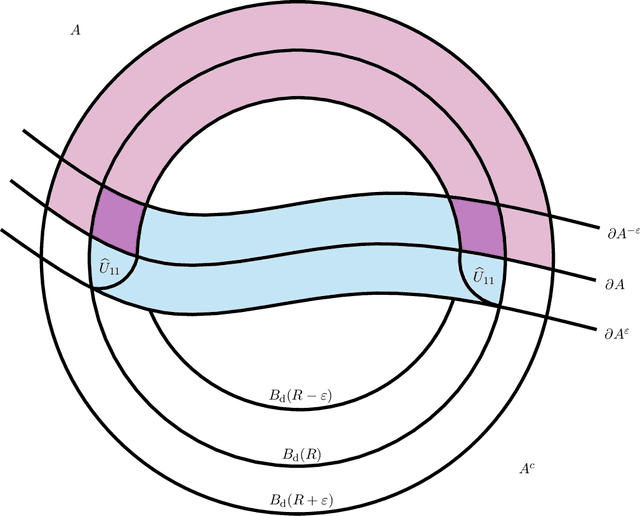

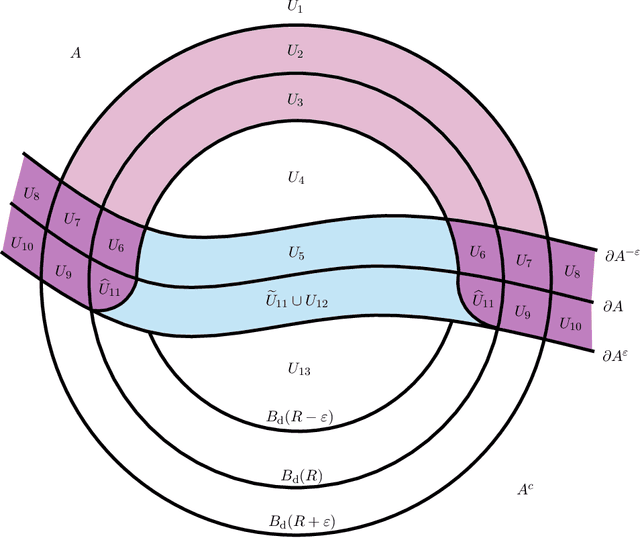
Abstract:In recent years there has been significant interest in the effect of different types of adversarial perturbations in data classification problems. Many of these models incorporate the adversarial power, which is an important parameter with an associated trade-off between accuracy and robustness. This work considers a general framework for adversarially-perturbed classification problems, in a large data or population-level limit. In such a regime, we demonstrate that as adversarial strength goes to zero that optimal classifiers converge to the Bayes classifier in the Hausdorff distance. This significantly strengthens previous results, which generally focus on $L^1$-type convergence. The main argument relies upon direct geometric comparisons and is inspired by techniques from geometric measure theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge