Evaluating generative networks using Gaussian mixtures of image features

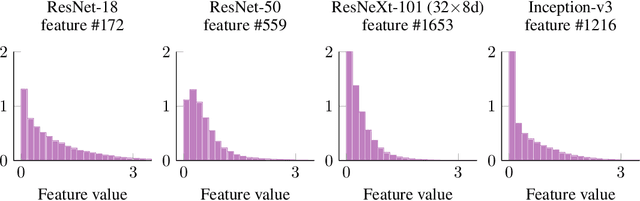
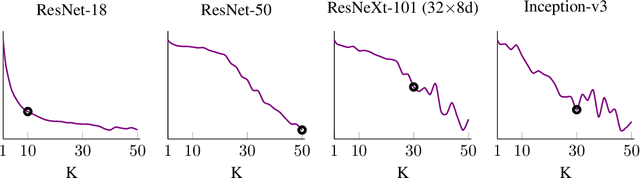
We develop a measure for evaluating the performance of generative networks given two sets of images. A popular performance measure currently used to do this is the Fr\'echet Inception Distance (FID). However, FID assumes that images featurized using the penultimate layer of Inception-v3 follow a Gaussian distribution. This assumption allows FID to be easily computed, since FID uses the 2-Wasserstein distance of two Gaussian distributions fitted to the featurized images. However, we show that Inception-v3 features of the ImageNet dataset are not Gaussian; in particular, each marginal is not Gaussian. To remedy this problem, we model the featurized images using Gaussian mixture models (GMMs) and compute the 2-Wasserstein distance restricted to GMMs. We define a performance measure, which we call WaM, on two sets of images by using Inception-v3 (or another classifier) to featurize the images, estimate two GMMs, and use the restricted 2-Wasserstein distance to compare the GMMs. We experimentally show the advantages of WaM over FID, including how FID is more sensitive than WaM to image perturbations. By modelling the non-Gaussian features obtained from Inception-v3 as GMMs and using a GMM metric, we can more accurately evaluate generative network performance.

The Outer Product Structure of Neural Network Derivatives

In this paper, we show that feedforward and recurrent neural networks exhibit an outer product derivative structure but that convolutional neural networks do not. This structure makes it possible to use higher-order information without needing approximations or infeasibly large amounts of memory, and it may also provide insights into the geometry of neural network optima. The ability to easily access these derivatives also suggests a new, geometric approach to regularization. We then discuss how this structure could be used to improve training methods, increase network robustness and generalizability, and inform network compression methods.

Multi-modal Geolocation Estimation Using Deep Neural Networks

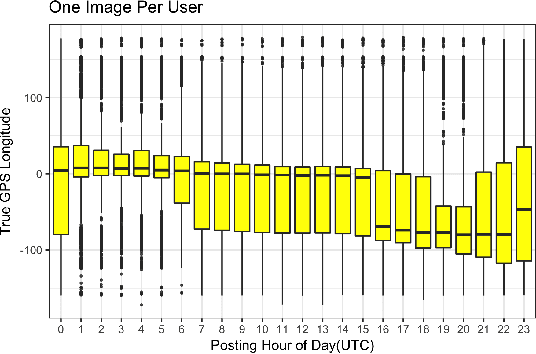
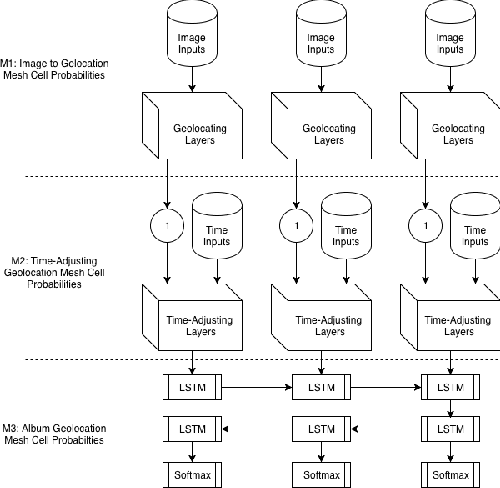
Estimating the location where an image was taken based solely on the contents of the image is a challenging task, even for humans, as properly labeling an image in such a fashion relies heavily on contextual information, and is not as simple as identifying a single object in the image. Thus any methods which attempt to do so must somehow account for these complexities, and no single model to date is completely capable of addressing all challenges. This work contributes to the state of research in image geolocation inferencing by introducing a novel global meshing strategy, outlining a variety of training procedures to overcome the considerable data limitations when training these models, and demonstrating how incorporating additional information can be used to improve the overall performance of a geolocation inference model. In this work, it is shown that Delaunay triangles are an effective type of mesh for geolocation in relatively low volume scenarios when compared to results from state of the art models which use quad trees and an order of magnitude more training data. In addition, the time of posting, learned user albuming, and other meta data are easily incorporated to improve geolocation by up to 11% for country-level (750 km) locality accuracy to 3% for city-level (25 km) localities.