Craig Bakker
Leveraging Structured Biological Knowledge for Counterfactual Inference: a Case Study of Viral Pathogenesis
Jan 13, 2021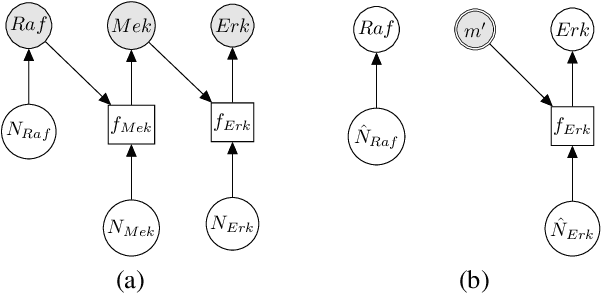
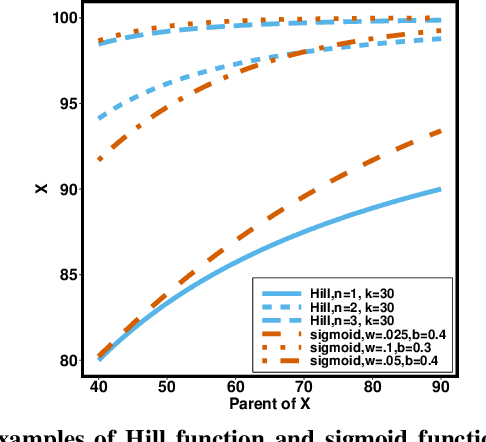

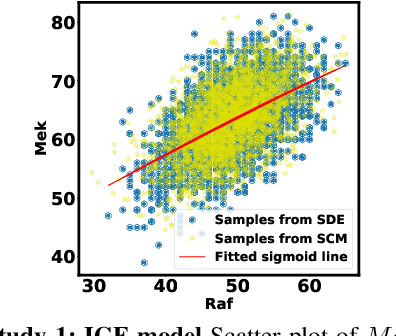
Abstract:Counterfactual inference is a useful tool for comparing outcomes of interventions on complex systems. It requires us to represent the system in form of a structural causal model, complete with a causal diagram, probabilistic assumptions on exogenous variables, and functional assignments. Specifying such models can be extremely difficult in practice. The process requires substantial domain expertise, and does not scale easily to large systems, multiple systems, or novel system modifications. At the same time, many application domains, such as molecular biology, are rich in structured causal knowledge that is qualitative in nature. This manuscript proposes a general approach for querying a causal biological knowledge graph, and converting the qualitative result into a quantitative structural causal model that can learn from data to answer the question. We demonstrate the feasibility, accuracy and versatility of this approach using two case studies in systems biology. The first demonstrates the appropriateness of the underlying assumptions and the accuracy of the results. The second demonstrates the versatility of the approach by querying a knowledge base for the molecular determinants of a severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2)-induced cytokine storm, and performing counterfactual inference to estimate the causal effect of medical countermeasures for severely ill patients.
Koopman Representations of Dynamic Systems with Control
Aug 06, 2019Abstract:The design and analysis of optimal control policies for dynamical systems can be complicated by nonlinear dependence in the state variables. Koopman operators have been used to simplify the analysis of dynamical systems by mapping the flow of the system onto a space of observables where the dynamics are linear (and possibly infinte). This paper focuses on the development of consistent Koopman representations for controlled dynamical system. We introduce the concept of dynamical consistency for Koopman representations and analyze several existing and proposed representations deriving necessary constraints on the dynamical system, observables, and Koopman operators. Our main result is a hybrid formulation which independently and jointly observes the state and control inputs. This formulation admits a relatively large space of dynamical systems compared to earlier formulations while keeping the Koopman operator independent of the state and control inputs. More generally, this work provides an analysis framework to evaluate and rank proposed simplifications to the general Koopman representation for controlled dynamical systems.
The Outer Product Structure of Neural Network Derivatives
Oct 09, 2018Abstract:In this paper, we show that feedforward and recurrent neural networks exhibit an outer product derivative structure but that convolutional neural networks do not. This structure makes it possible to use higher-order information without needing approximations or infeasibly large amounts of memory, and it may also provide insights into the geometry of neural network optima. The ability to easily access these derivatives also suggests a new, geometric approach to regularization. We then discuss how this structure could be used to improve training methods, increase network robustness and generalizability, and inform network compression methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge