Koopman Representations of Dynamic Systems with Control

The design and analysis of optimal control policies for dynamical systems can be complicated by nonlinear dependence in the state variables. Koopman operators have been used to simplify the analysis of dynamical systems by mapping the flow of the system onto a space of observables where the dynamics are linear (and possibly infinte). This paper focuses on the development of consistent Koopman representations for controlled dynamical system. We introduce the concept of dynamical consistency for Koopman representations and analyze several existing and proposed representations deriving necessary constraints on the dynamical system, observables, and Koopman operators. Our main result is a hybrid formulation which independently and jointly observes the state and control inputs. This formulation admits a relatively large space of dynamical systems compared to earlier formulations while keeping the Koopman operator independent of the state and control inputs. More generally, this work provides an analysis framework to evaluate and rank proposed simplifications to the general Koopman representation for controlled dynamical systems.

Relative Hausdorff Distance for Network Analysis

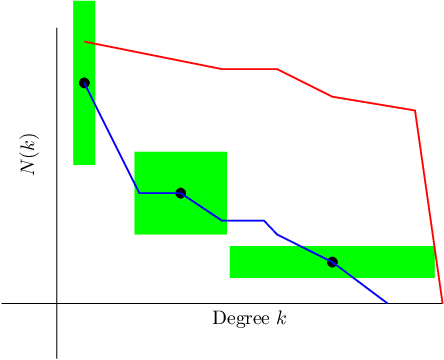
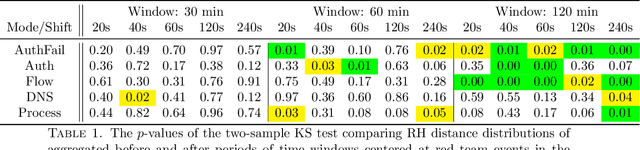
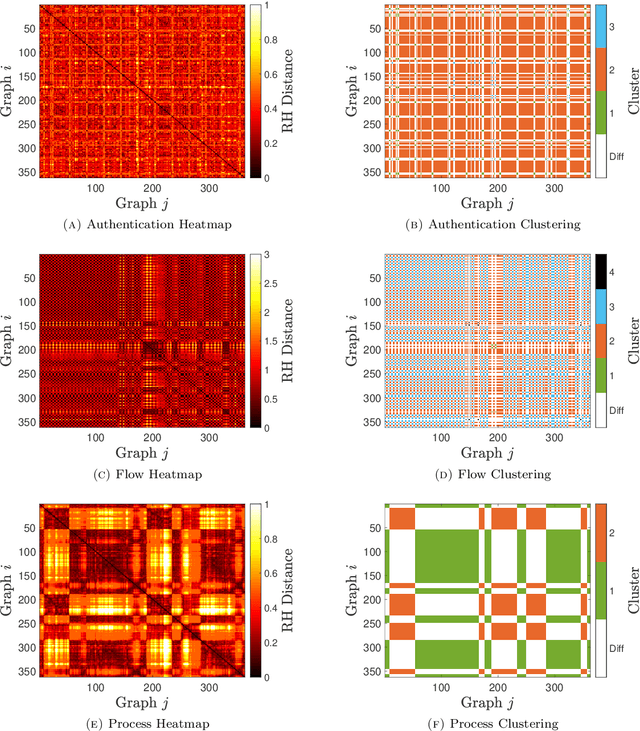
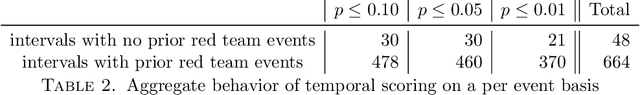
Similarity measures are used extensively in machine learning and data science algorithms. The newly proposed graph Relative Hausdorff (RH) distance is a lightweight yet nuanced similarity measure for quantifying the closeness of two graphs. In this work we study the effectiveness of RH distance as a tool for detecting anomalies in time-evolving graph sequences. We apply RH to cyber data with given red team events, as well to synthetically generated sequences of graphs with planted attacks. In our experiments, the performance of RH distance is at times comparable, and sometimes superior, to graph edit distance in detecting anomalous phenomena. Our results suggest that in appropriate contexts, RH distance has advantages over more computationally intensive similarity measures.