Pavan K. Kota
Extreme Compressed Sensing of Poisson Rates from Multiple Measurements
Mar 15, 2021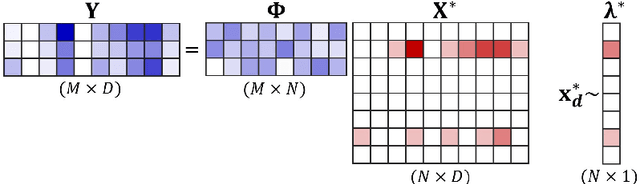
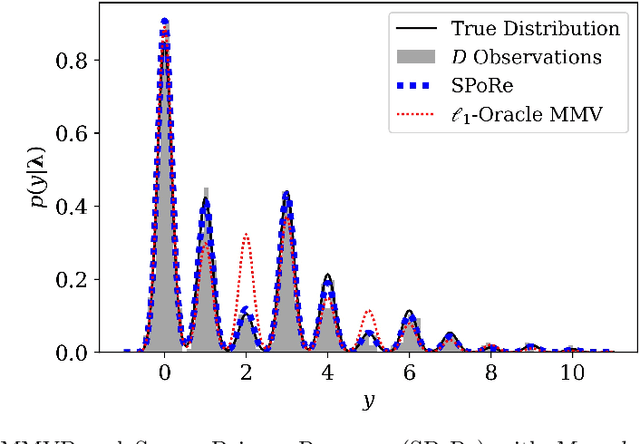
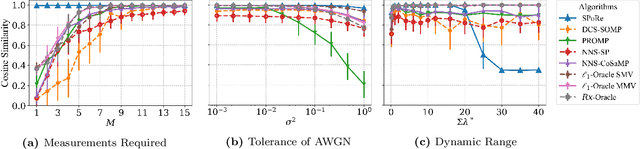
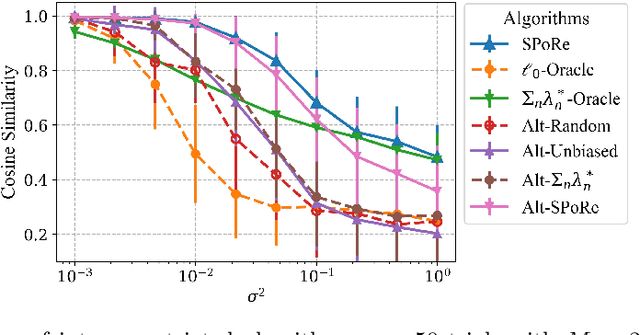
Abstract:Compressed sensing (CS) is a signal processing technique that enables the efficient recovery of a sparse high-dimensional signal from low-dimensional measurements. In the multiple measurement vector (MMV) framework, a set of signals with the same support must be recovered from their corresponding measurements. Here, we present the first exploration of the MMV problem where signals are independently drawn from a sparse, multivariate Poisson distribution. We are primarily motivated by a suite of biosensing applications of microfluidics where analytes (such as whole cells or biomarkers) are captured in small volume partitions according to a Poisson distribution. We recover the sparse parameter vector of Poisson rates through maximum likelihood estimation with our novel Sparse Poisson Recovery (SPoRe) algorithm. SPoRe uses batch stochastic gradient ascent enabled by Monte Carlo approximations of otherwise intractable gradients. By uniquely leveraging the Poisson structure, SPoRe substantially outperforms a comprehensive set of existing and custom baseline CS algorithms. Notably, SPoRe can exhibit high performance even with one-dimensional measurements and high noise levels. This resource efficiency is not only unprecedented in the field of CS but is also particularly potent for applications in microfluidics in which the number of resolvable measurements per partition is often severely limited. We prove the identifiability property of the Poisson model under such lax conditions, analytically develop insights into system performance, and confirm these insights in simulated experiments. Our findings encourage a new approach to biosensing and are generalizable to other applications featuring spatial and temporal Poisson signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge