cryoSENSE: Compressive Sensing Enables High-throughput Microscopy with Sparse and Generative Priors on the Protein Cryo-EM Image Manifold

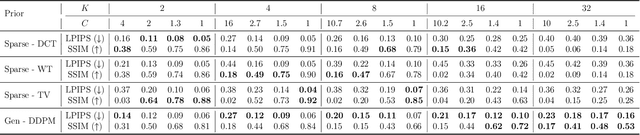
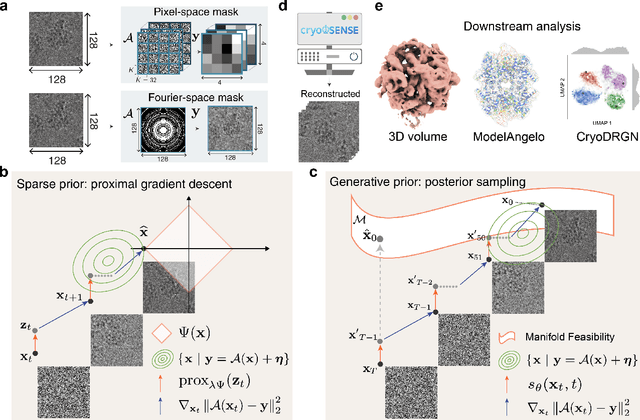
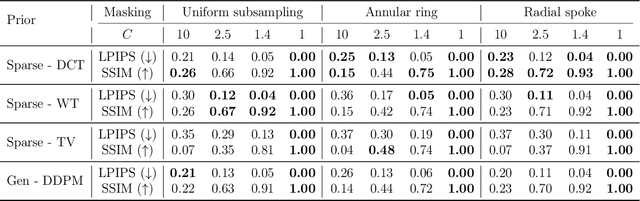
Cryo-electron microscopy (cryo-EM) enables the atomic-resolution visualization of biomolecules; however, modern direct detectors generate data volumes that far exceed the available storage and transfer bandwidth, thereby constraining practical throughput. We introduce cryoSENSE, the computational realization of a hardware-software co-designed framework for compressive cryo-EM sensing and acquisition. We show that cryo-EM images of proteins lie on low-dimensional manifolds that can be independently represented using sparse priors in predefined bases and generative priors captured by a denoising diffusion model. cryoSENSE leverages these low-dimensional manifolds to enable faithful image reconstruction from spatial and Fourier-domain undersampled measurements while preserving downstream structural resolution. In experiments, cryoSENSE increases acquisition throughput by up to 2.5$\times$ while retaining the original 3D resolution, offering controllable trade-offs between the number of masked measurements and the level of downsampling. Sparse priors favor faithful reconstruction from Fourier-domain measurements and moderate compression, whereas generative diffusion priors achieve accurate recovery from pixel-domain measurements and more severe undersampling. Project website: https://cryosense.github.io.

Efficient Algorithm for Sparse Fourier Transform of Generalized q-ary Functions

Computing the Fourier transform of a $q$-ary function $f:\mathbb{Z}_{q}^n\rightarrow \mathbb{R}$, which maps $q$-ary sequences to real numbers, is an important problem in mathematics with wide-ranging applications in biology, signal processing, and machine learning. Previous studies have shown that, under the sparsity assumption, the Fourier transform can be computed efficiently using fast and sample-efficient algorithms. However, in many practical settings, the function is defined over a more general space -- the space of generalized $q$-ary sequences $\mathbb{Z}_{q_1} \times \mathbb{Z}_{q_2} \times \cdots \times \mathbb{Z}_{q_n}$ -- where each $\mathbb{Z}_{q_i}$ corresponds to integers modulo $q_i$. A naive approach involves setting $q=\max_i{q_i}$ and treating the function as $q$-ary, which results in heavy computational overheads. Herein, we develop GFast, an algorithm that computes the $S$-sparse Fourier transform of $f$ with a sample complexity of $O(Sn)$, computational complexity of $O(Sn \log N)$, and a failure probability that approaches zero as $N=\prod_{i=1}^n q_i \rightarrow \infty$ with $S = N^\delta$ for some $0 \leq \delta < 1$. In the presence of noise, we further demonstrate that a robust version of GFast computes the transform with a sample complexity of $O(Sn^2)$ and computational complexity of $O(Sn^2 \log N)$ under the same high probability guarantees. Using large-scale synthetic experiments, we demonstrate that GFast computes the sparse Fourier transform of generalized $q$-ary functions using $16\times$ fewer samples and running $8\times$ faster than existing algorithms. In real-world protein fitness datasets, GFast explains the predictive interactions of a neural network with $>25\%$ smaller normalized mean-squared error compared to existing algorithms.

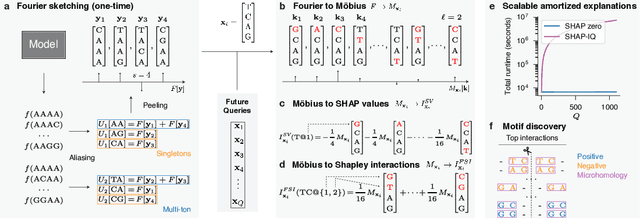
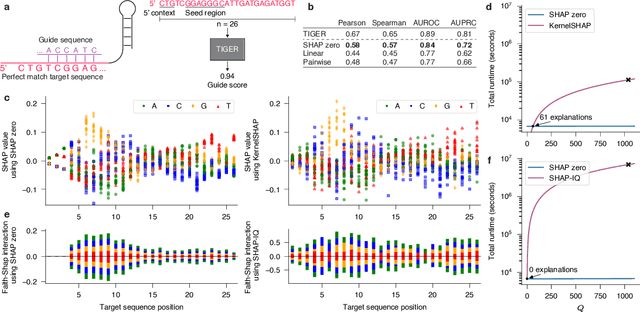
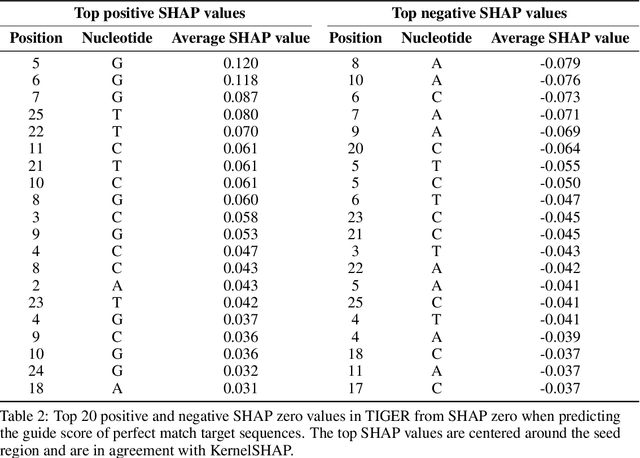
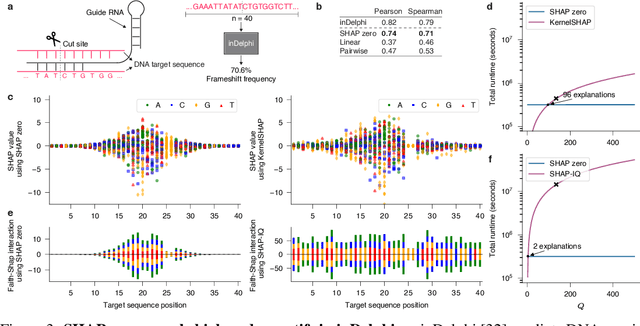
SHAP zero Explains All-order Feature Interactions in Black-box Genomic Models with Near-zero Query Cost

With the rapid growth of black-box models in machine learning, Shapley values have emerged as a popular method for model explanations due to their theoretical guarantees. Shapley values locally explain a model to an input query using additive features. Yet, in genomics, extracting biological knowledge from black-box models hinges on explaining nonlinear feature interactions globally to hundreds to thousands of input query sequences. Herein, we develop SHAP zero, an algorithm that estimates all-order Shapley feature interactions with a near-zero cost per queried sequence after paying a one-time fee for model sketching. SHAP zero achieves this by establishing a surprisingly underexplored connection between the Shapley interactions and the Fourier transform of the model. Explaining two genomic models, one trained to predict guide RNA binding and the other to predict DNA repair outcomes, we demonstrate that SHAP zero achieves orders of magnitude reduction in amortized computational cost compared to state-of-the-art algorithms. SHAP zero reveals all microhomologous motifs that are predictive of DNA repair outcome, a finding previously inaccessible due to the combinatorial space of possible high-order feature interactions.