BEAR: Sketching BFGS Algorithm for Ultra-High Dimensional Feature Selection in Sublinear Memory
Paper and Code
Oct 26, 2020
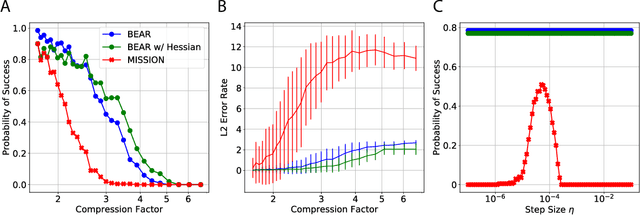

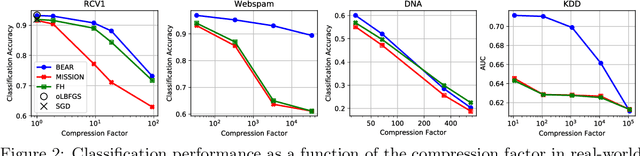
We consider feature selection for applications in machine learning where the dimensionality of the data is so large that it exceeds the working memory of the (local) computing machine. Unfortunately, current large-scale sketching algorithms show poor memory-accuracy trade-off due to the irreversible collision and accumulation of the stochastic gradient noise in the sketched domain. Here, we develop a second-order ultra-high dimensional feature selection algorithm, called BEAR, which avoids the extra collisions by storing the second-order gradients in the celebrated Broyden-Fletcher-Goldfarb-Shannon (BFGS) algorithm in Count Sketch, a sublinear memory data structure from the streaming literature. Experiments on real-world data sets demonstrate that BEAR requires up to three orders of magnitude less memory space to achieve the same classification accuracy compared to the first-order sketching algorithms. Theoretical analysis proves convergence of BEAR with rate O(1/t) in t iterations of the sketched algorithm. Our algorithm reveals an unexplored advantage of second-order optimization for memory-constrained sketching of models trained on ultra-high dimensional data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge