Locally Interdependent Multi-Agent MDP: Theoretical Framework for Decentralized Agents with Dynamic Dependencies

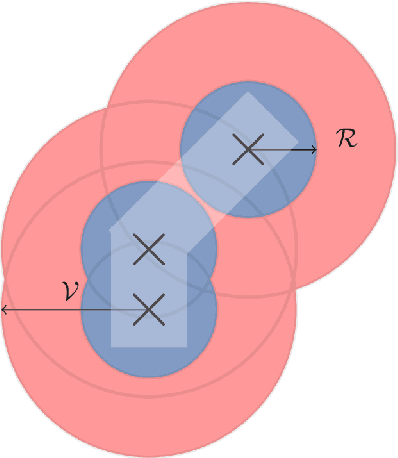
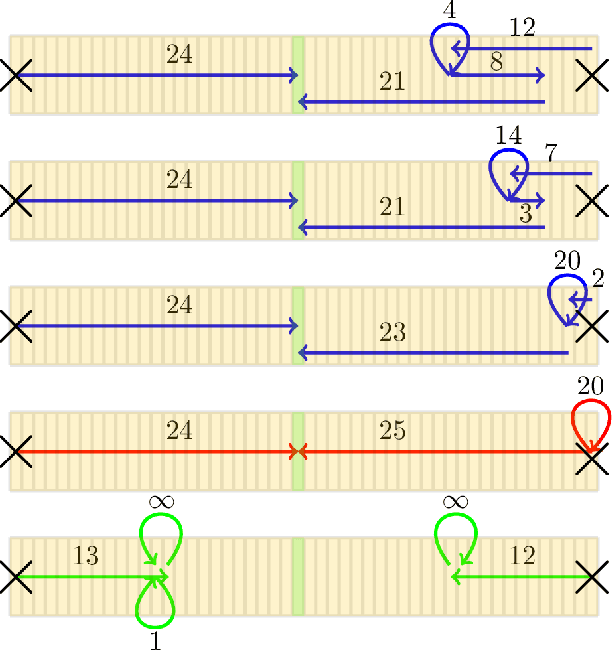
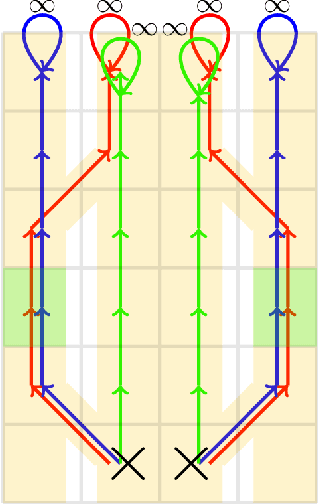
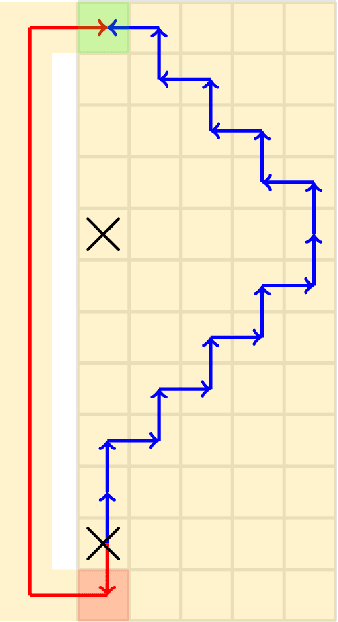
Many multi-agent systems in practice are decentralized and have dynamically varying dependencies. There has been a lack of attempts in the literature to analyze these systems theoretically. In this paper, we propose and theoretically analyze a decentralized model with dynamically varying dependencies called the Locally Interdependent Multi-Agent MDP. This model can represent problems in many disparate domains such as cooperative navigation, obstacle avoidance, and formation control. Despite the intractability that general partially observable multi-agent systems suffer from, we propose three closed-form policies that are theoretically near-optimal in this setting and can be scalable to compute and store. Consequentially, we reveal a fundamental property of Locally Interdependent Multi-Agent MDP's that the partially observable decentralized solution is exponentially close to the fully observable solution with respect to the visibility radius. We then discuss extensions of our closed-form policies to further improve tractability. We conclude by providing simulations to investigate some long horizon behaviors of our closed-form policies.

BEAR: Sketching BFGS Algorithm for Ultra-High Dimensional Feature Selection in Sublinear Memory

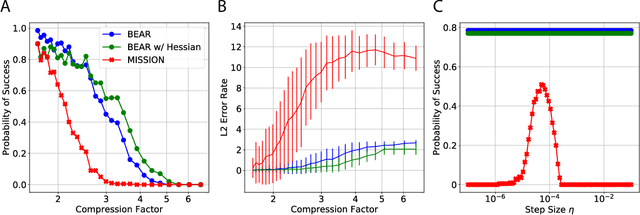
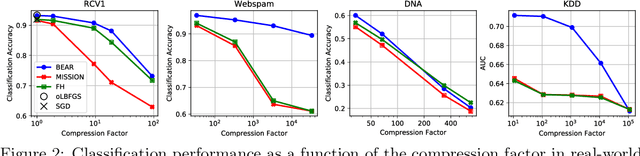
We consider feature selection for applications in machine learning where the dimensionality of the data is so large that it exceeds the working memory of the (local) computing machine. Unfortunately, current large-scale sketching algorithms show poor memory-accuracy trade-off due to the irreversible collision and accumulation of the stochastic gradient noise in the sketched domain. Here, we develop a second-order ultra-high dimensional feature selection algorithm, called BEAR, which avoids the extra collisions by storing the second-order gradients in the celebrated Broyden-Fletcher-Goldfarb-Shannon (BFGS) algorithm in Count Sketch, a sublinear memory data structure from the streaming literature. Experiments on real-world data sets demonstrate that BEAR requires up to three orders of magnitude less memory space to achieve the same classification accuracy compared to the first-order sketching algorithms. Theoretical analysis proves convergence of BEAR with rate O(1/t) in t iterations of the sketched algorithm. Our algorithm reveals an unexplored advantage of second-order optimization for memory-constrained sketching of models trained on ultra-high dimensional data sets.