BEAR: Sketching BFGS Algorithm for Ultra-High Dimensional Feature Selection in Sublinear Memory

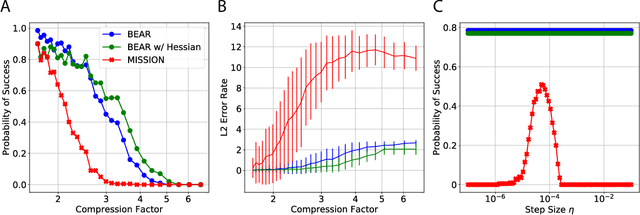
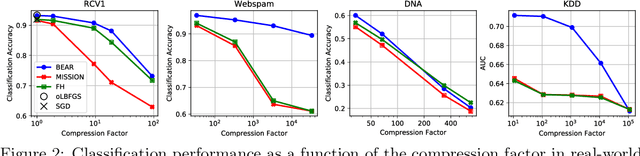
We consider feature selection for applications in machine learning where the dimensionality of the data is so large that it exceeds the working memory of the (local) computing machine. Unfortunately, current large-scale sketching algorithms show poor memory-accuracy trade-off due to the irreversible collision and accumulation of the stochastic gradient noise in the sketched domain. Here, we develop a second-order ultra-high dimensional feature selection algorithm, called BEAR, which avoids the extra collisions by storing the second-order gradients in the celebrated Broyden-Fletcher-Goldfarb-Shannon (BFGS) algorithm in Count Sketch, a sublinear memory data structure from the streaming literature. Experiments on real-world data sets demonstrate that BEAR requires up to three orders of magnitude less memory space to achieve the same classification accuracy compared to the first-order sketching algorithms. Theoretical analysis proves convergence of BEAR with rate O(1/t) in t iterations of the sketched algorithm. Our algorithm reveals an unexplored advantage of second-order optimization for memory-constrained sketching of models trained on ultra-high dimensional data sets.

FastSecAgg: Scalable Secure Aggregation for Privacy-Preserving Federated Learning

Recent attacks on federated learning demonstrate that keeping the training data on clients' devices does not provide sufficient privacy, as the model parameters shared by clients can leak information about their training data. A 'secure aggregation' protocol enables the server to aggregate clients' models in a privacy-preserving manner. However, existing secure aggregation protocols incur high computation/communication costs, especially when the number of model parameters is larger than the number of clients participating in an iteration -- a typical scenario in federated learning. In this paper, we propose a secure aggregation protocol, FastSecAgg, that is efficient in terms of computation and communication, and robust to client dropouts. The main building block of FastSecAgg is a novel multi-secret sharing scheme, FastShare, based on the Fast Fourier Transform (FFT), which may be of independent interest. FastShare is information-theoretically secure, and achieves a trade-off between the number of secrets, privacy threshold, and dropout tolerance. Riding on the capabilities of FastShare, we prove that FastSecAgg is (i) secure against the server colluding with 'any' subset of some constant fraction (e.g. $\sim10\%$) of the clients in the honest-but-curious setting; and (ii) tolerates dropouts of a 'random' subset of some constant fraction (e.g. $\sim10\%$) of the clients. FastSecAgg achieves significantly smaller computation cost than existing schemes while achieving the same (orderwise) communication cost. In addition, it guarantees security against adaptive adversaries, which can perform client corruptions dynamically during the execution of the protocol.

Communication-Efficient Gradient Coding for Straggler Mitigation in Distributed Learning

Distributed implementations of gradient-based methods, wherein a server distributes gradient computations across worker machines, need to overcome two limitations: delays caused by slow running machines called 'stragglers', and communication overheads. Recently, Ye and Abbe [ICML 2018] proposed a coding-theoretic paradigm to characterize a fundamental trade-off between computation load per worker, communication overhead per worker, and straggler tolerance. However, their proposed coding schemes suffer from heavy decoding complexity and poor numerical stability. In this paper, we develop a communication-efficient gradient coding framework to overcome these drawbacks. Our proposed framework enables using any linear code to design the encoding and decoding functions. When a particular code is used in this framework, its block-length determines the computation load, dimension determines the communication overhead, and minimum distance determines the straggler tolerance. The flexibility of choosing a code allows us to gracefully trade-off the straggler threshold and communication overhead for smaller decoding complexity and higher numerical stability. Further, we show that using a maximum distance separable (MDS) code generated by a random Gaussian matrix in our framework yields a gradient code that is optimal with respect to the trade-off and, in addition, satisfies stronger guarantees on numerical stability as compared to the previously proposed schemes. Finally, we evaluate our proposed framework on Amazon EC2 and demonstrate that it reduces the average iteration time by 16% as compared to prior gradient coding schemes.

Gradient Coding Based on Block Designs for Mitigating Adversarial Stragglers

Distributed implementations of gradient-based methods, wherein a server distributes gradient computations across worker machines, suffer from slow running machines, called 'stragglers'. Gradient coding is a coding-theoretic framework to mitigate stragglers by enabling the server to recover the gradient sum in the presence of stragglers. 'Approximate gradient codes' are variants of gradient codes that reduce computation and storage overhead per worker by allowing the server to approximately reconstruct the gradient sum. In this work, our goal is to construct approximate gradient codes that are resilient to stragglers selected by a computationally unbounded adversary. Our motivation for constructing codes to mitigate adversarial stragglers stems from the challenge of tackling stragglers in massive-scale elastic and serverless systems, wherein it is difficult to statistically model stragglers. Towards this end, we propose a class of approximate gradient codes based on balanced incomplete block designs (BIBDs). We show that the approximation error for these codes depends only on the number of stragglers, and thus, adversarial straggler selection has no advantage over random selection. In addition, the proposed codes admit computationally efficient decoding at the server. Next, to characterize fundamental limits of adversarial straggling, we consider the notion of 'adversarial threshold' -- the smallest number of workers that an adversary must straggle to inflict certain approximation error. We compute a lower bound on the adversarial threshold, and show that codes based on symmetric BIBDs maximize this lower bound among a wide class of codes, making them excellent candidates for mitigating adversarial stragglers.

On the organization of grid and place cells: Neural de-noising via subspace learning

Place cells in the hippocampus are active when an animal visits a certain location (referred to as a place field) within an environment. Grid cells in the medial entorhinal cortex (MEC) respond at multiple locations, with firing fields that form a periodic and hexagonal tiling of the environment. The joint activity of grid and place cell populations, as a function of location, forms a neural code for space. An ensemble of codes is generated by varying grid and place cell population parameters. For each code in this ensemble, codewords are generated by stimulating a network with a discrete set of locations. In this manuscript, we develop an understanding of the relationships between coding theoretic properties of these combined populations and code construction parameters. These relationships are revisited by measuring the performances of biologically realizable algorithms implemented by networks of place and grid cell populations, as well as constraint neurons, which perform de-noising operations. Objectives of this work include the investigation of coding theoretic limitations of the mammalian neural code for location and how communication between grid and place cell networks may improve the accuracy of each population's representation. Simulations demonstrate that de-noising mechanisms analyzed here can significantly improve fidelity of this neural representation of space. Further, patterns observed in connectivity of each population of simulated cells suggest that inter-hippocampal-medial-entorhinal-cortical connectivity decreases downward along the dorsoventral axis.