Swanand Kadhe
Protecting Users From Themselves: Safeguarding Contextual Privacy in Interactions with Conversational Agents
Feb 22, 2025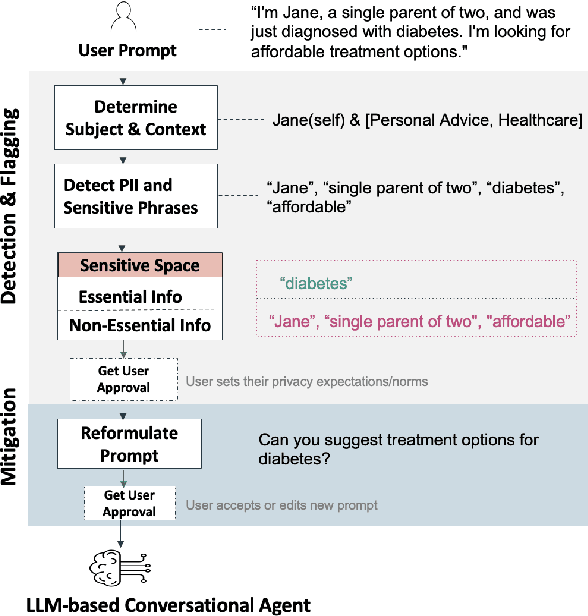

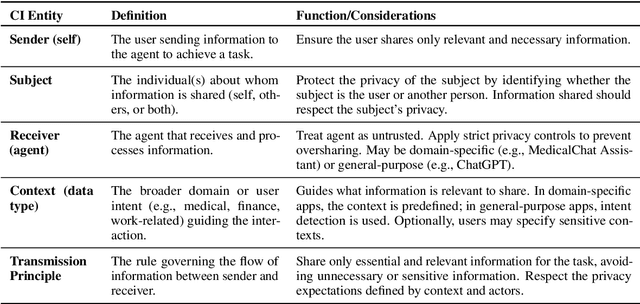
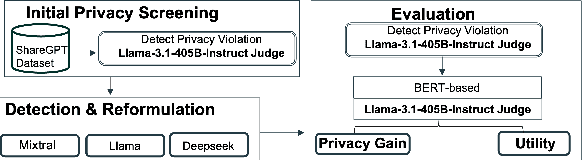
Abstract:Conversational agents are increasingly woven into individuals' personal lives, yet users often underestimate the privacy risks involved. The moment users share information with these agents (e.g., LLMs), their private information becomes vulnerable to exposure. In this paper, we characterize the notion of contextual privacy for user interactions with LLMs. It aims to minimize privacy risks by ensuring that users (sender) disclose only information that is both relevant and necessary for achieving their intended goals when interacting with LLMs (untrusted receivers). Through a formative design user study, we observe how even "privacy-conscious" users inadvertently reveal sensitive information through indirect disclosures. Based on insights from this study, we propose a locally-deployable framework that operates between users and LLMs, and identifies and reformulates out-of-context information in user prompts. Our evaluation using examples from ShareGPT shows that lightweight models can effectively implement this framework, achieving strong gains in contextual privacy while preserving the user's intended interaction goals through different approaches to classify information relevant to the intended goals.
LESS-VFL: Communication-Efficient Feature Selection for Vertical Federated Learning
May 03, 2023



Abstract:We propose LESS-VFL, a communication-efficient feature selection method for distributed systems with vertically partitioned data. We consider a system of a server and several parties with local datasets that share a sample ID space but have different feature sets. The parties wish to collaboratively train a model for a prediction task. As part of the training, the parties wish to remove unimportant features in the system to improve generalization, efficiency, and explainability. In LESS-VFL, after a short pre-training period, the server optimizes its part of the global model to determine the relevant outputs from party models. This information is shared with the parties to then allow local feature selection without communication. We analytically prove that LESS-VFL removes spurious features from model training. We provide extensive empirical evidence that LESS-VFL can achieve high accuracy and remove spurious features at a fraction of the communication cost of other feature selection approaches.
Robust Learning Protocol for Federated Tumor Segmentation Challenge
Dec 16, 2022Abstract:In this work, we devise robust and efficient learning protocols for orchestrating a Federated Learning (FL) process for the Federated Tumor Segmentation Challenge (FeTS 2022). Enabling FL for FeTS setup is challenging mainly due to data heterogeneity among collaborators and communication cost of training. To tackle these challenges, we propose Robust Learning Protocol (RoLePRO) which is a combination of server-side adaptive optimisation (e.g., server-side Adam) and judicious parameter (weights) aggregation schemes (e.g., adaptive weighted aggregation). RoLePRO takes a two-phase approach, where the first phase consists of vanilla Federated Averaging, while the second phase consists of a judicious aggregation scheme that uses a sophisticated reweighting, all in the presence of an adaptive optimisation algorithm at the server. We draw insights from extensive experimentation to tune learning rates for the two phases.
Federated Unlearning: How to Efficiently Erase a Client in FL?
Jul 12, 2022
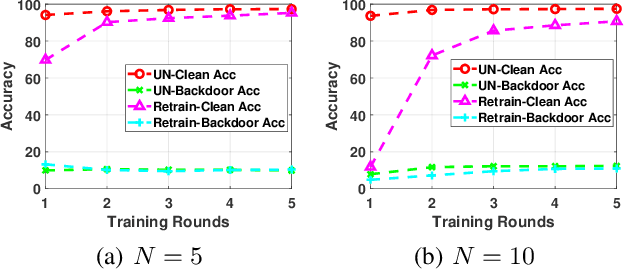
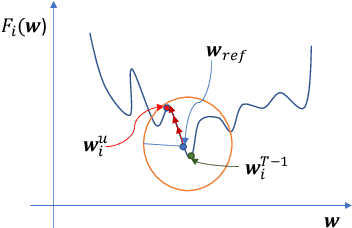
Abstract:With privacy legislation empowering users with the right to be forgotten, it has become essential to make a model forget about some of its training data. We explore the problem of removing any client's contribution in federated learning (FL). During FL rounds, each client performs local training to learn a model that minimizes the empirical loss on their private data. We propose to perform unlearning at the client (to be erased) by reversing the learning process, i.e., training a model to \emph{maximize} the local empirical loss. In particular, we formulate the unlearning problem as a constrained maximization problem by restricting to an $\ell_2$-norm ball around a suitably chosen reference model to help retain some knowledge learnt from the other clients' data. This allows the client to use projected gradient descent to perform unlearning. The method does neither require global access to the data used for training nor the history of the parameter updates to be stored by the aggregator (server) or any of the clients. Experiments on the MNIST dataset show that the proposed unlearning method is efficient and effective.
Leveraging Spatial and Temporal Correlations in Sparsified Mean Estimation
Oct 14, 2021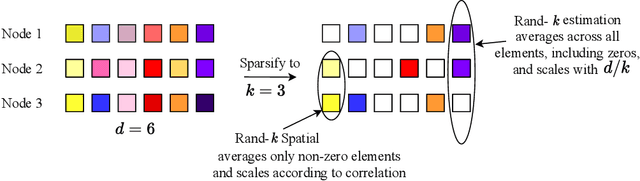
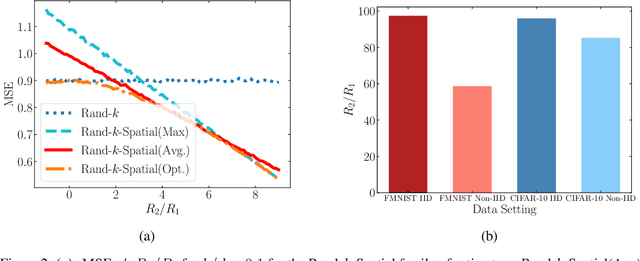
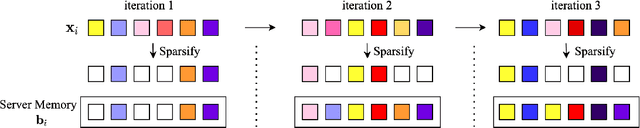
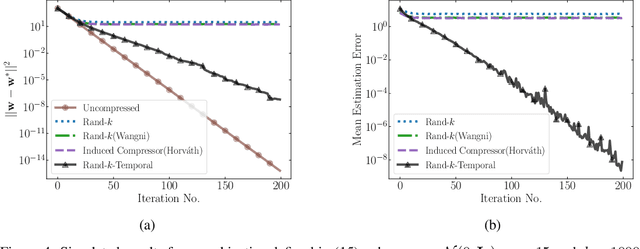
Abstract:We study the problem of estimating at a central server the mean of a set of vectors distributed across several nodes (one vector per node). When the vectors are high-dimensional, the communication cost of sending entire vectors may be prohibitive, and it may be imperative for them to use sparsification techniques. While most existing work on sparsified mean estimation is agnostic to the characteristics of the data vectors, in many practical applications such as federated learning, there may be spatial correlations (similarities in the vectors sent by different nodes) or temporal correlations (similarities in the data sent by a single node over different iterations of the algorithm) in the data vectors. We leverage these correlations by simply modifying the decoding method used by the server to estimate the mean. We provide an analysis of the resulting estimation error as well as experiments for PCA, K-Means and Logistic Regression, which show that our estimators consistently outperform more sophisticated and expensive sparsification methods.
FastSecAgg: Scalable Secure Aggregation for Privacy-Preserving Federated Learning
Sep 23, 2020



Abstract:Recent attacks on federated learning demonstrate that keeping the training data on clients' devices does not provide sufficient privacy, as the model parameters shared by clients can leak information about their training data. A 'secure aggregation' protocol enables the server to aggregate clients' models in a privacy-preserving manner. However, existing secure aggregation protocols incur high computation/communication costs, especially when the number of model parameters is larger than the number of clients participating in an iteration -- a typical scenario in federated learning. In this paper, we propose a secure aggregation protocol, FastSecAgg, that is efficient in terms of computation and communication, and robust to client dropouts. The main building block of FastSecAgg is a novel multi-secret sharing scheme, FastShare, based on the Fast Fourier Transform (FFT), which may be of independent interest. FastShare is information-theoretically secure, and achieves a trade-off between the number of secrets, privacy threshold, and dropout tolerance. Riding on the capabilities of FastShare, we prove that FastSecAgg is (i) secure against the server colluding with 'any' subset of some constant fraction (e.g. $\sim10\%$) of the clients in the honest-but-curious setting; and (ii) tolerates dropouts of a 'random' subset of some constant fraction (e.g. $\sim10\%$) of the clients. FastSecAgg achieves significantly smaller computation cost than existing schemes while achieving the same (orderwise) communication cost. In addition, it guarantees security against adaptive adversaries, which can perform client corruptions dynamically during the execution of the protocol.
Communication-Efficient Gradient Coding for Straggler Mitigation in Distributed Learning
May 14, 2020


Abstract:Distributed implementations of gradient-based methods, wherein a server distributes gradient computations across worker machines, need to overcome two limitations: delays caused by slow running machines called 'stragglers', and communication overheads. Recently, Ye and Abbe [ICML 2018] proposed a coding-theoretic paradigm to characterize a fundamental trade-off between computation load per worker, communication overhead per worker, and straggler tolerance. However, their proposed coding schemes suffer from heavy decoding complexity and poor numerical stability. In this paper, we develop a communication-efficient gradient coding framework to overcome these drawbacks. Our proposed framework enables using any linear code to design the encoding and decoding functions. When a particular code is used in this framework, its block-length determines the computation load, dimension determines the communication overhead, and minimum distance determines the straggler tolerance. The flexibility of choosing a code allows us to gracefully trade-off the straggler threshold and communication overhead for smaller decoding complexity and higher numerical stability. Further, we show that using a maximum distance separable (MDS) code generated by a random Gaussian matrix in our framework yields a gradient code that is optimal with respect to the trade-off and, in addition, satisfies stronger guarantees on numerical stability as compared to the previously proposed schemes. Finally, we evaluate our proposed framework on Amazon EC2 and demonstrate that it reduces the average iteration time by 16% as compared to prior gradient coding schemes.
Communication-Efficient and Byzantine-Robust Distributed Learning
Nov 21, 2019



Abstract:We develop a communication-efficient distributed learning algorithm that is robust against Byzantine worker machines. We propose and analyze a distributed gradient-descent algorithm that performs a simple thresholding based on gradient norms to mitigate Byzantine failures. We show the (statistical) error-rate of our algorithm matches that of [YCKB18], which uses more complicated schemes (like coordinate-wise median or trimmed mean) and thus optimal. Furthermore, for communication efficiency, we consider a generic class of {\delta}-approximate compressors from [KRSJ19] that encompasses sign-based compressors and top-k sparsification. Our algorithm uses compressed gradients and gradient norms for aggregation and Byzantine removal respectively. We establish the statistical error rate of the algorithm for arbitrary (convex or non-convex) smooth loss function. We show that, in the regime when the compression factor {\delta} is constant and the dimension of the parameter space is fixed, the rate of convergence is not affected by the compression operation, and hence we effectively get the compression for free. Moreover, we extend the compressed gradient descent algorithm with error feedback proposed in [KRSJ19] for the distributed setting. We have experimentally validated our results and shown good performance in convergence for convex (least-square regression) and non-convex (neural network training) problems.
Gradient Coding Based on Block Designs for Mitigating Adversarial Stragglers
Apr 30, 2019



Abstract:Distributed implementations of gradient-based methods, wherein a server distributes gradient computations across worker machines, suffer from slow running machines, called 'stragglers'. Gradient coding is a coding-theoretic framework to mitigate stragglers by enabling the server to recover the gradient sum in the presence of stragglers. 'Approximate gradient codes' are variants of gradient codes that reduce computation and storage overhead per worker by allowing the server to approximately reconstruct the gradient sum. In this work, our goal is to construct approximate gradient codes that are resilient to stragglers selected by a computationally unbounded adversary. Our motivation for constructing codes to mitigate adversarial stragglers stems from the challenge of tackling stragglers in massive-scale elastic and serverless systems, wherein it is difficult to statistically model stragglers. Towards this end, we propose a class of approximate gradient codes based on balanced incomplete block designs (BIBDs). We show that the approximation error for these codes depends only on the number of stragglers, and thus, adversarial straggler selection has no advantage over random selection. In addition, the proposed codes admit computationally efficient decoding at the server. Next, to characterize fundamental limits of adversarial straggling, we consider the notion of 'adversarial threshold' -- the smallest number of workers that an adversary must straggle to inflict certain approximation error. We compute a lower bound on the adversarial threshold, and show that codes based on symmetric BIBDs maximize this lower bound among a wide class of codes, making them excellent candidates for mitigating adversarial stragglers.
OverSketched Newton: Fast Convex Optimization for Serverless Systems
Mar 21, 2019



Abstract:Motivated by recent developments in serverless systems for large-scale machine learning as well as improvements in scalable randomized matrix algorithms, we develop OverSketched Newton, a randomized Hessian-based optimization algorithm to solve large-scale smooth and strongly-convex problems in serverless systems. OverSketched Newton leverages matrix sketching ideas from Randomized Numerical Linear Algebra to compute the Hessian approximately. These sketching methods lead to inbuilt resiliency against stragglers that are a characteristic of serverless architectures. We establish that OverSketched Newton has a linear-quadratic convergence rate, and we empirically validate our results by solving large-scale supervised learning problems on real-world datasets. Experiments demonstrate a reduction of ~50% in total running time on AWS Lambda, compared to state-of-the-art distributed optimization schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge