NL2OR: Solve Complex Operations Research Problems Using Natural Language Inputs

Operations research (OR) uses mathematical models to enhance decision-making, but developing these models requires expert knowledge and can be time-consuming. Automated mathematical programming (AMP) has emerged to simplify this process, but existing systems have limitations. This paper introduces a novel methodology that uses recent advances in Large Language Model (LLM) to create and edit OR solutions from non-expert user queries expressed using Natural Language. This reduces the need for domain expertise and the time to formulate a problem. The paper presents an end-to-end pipeline, named NL2OR, that generates solutions to OR problems from natural language input, and shares experimental results on several important OR problems.

Escaping Saddle Points in Distributed Newton's Method with Communication efficiency and Byzantine Resilience

We study the problem of optimizing a non-convex loss function (with saddle points) in a distributed framework in the presence of Byzantine machines. We consider a standard distributed setting with one central machine (parameter server) communicating with many worker machines. Our proposed algorithm is a variant of the celebrated cubic-regularized Newton method of Nesterov and Polyak \cite{nest}, which avoids saddle points efficiently and converges to local minima. Furthermore, our algorithm resists the presence of Byzantine machines, which may create \emph{fake local minima} near the saddle points of the loss function, also known as saddle-point attack. We robustify the cubic-regularized Newton algorithm such that it avoids the saddle points and the fake local minimas efficiently. Furthermore, being a second order algorithm, the iteration complexity is much lower than its first order counterparts, and thus our algorithm communicates little with the parameter server. We obtain theoretical guarantees for our proposed scheme under several settings including approximate (sub-sampled) gradients and Hessians. Moreover, we validate our theoretical findings with experiments using standard datasets and several types of Byzantine attacks.

Estimation of Shortest Path Covariance Matrices

We study the sample complexity of estimating the covariance matrix $\mathbf{\Sigma} \in \mathbb{R}^{d\times d}$ of a distribution $\mathcal D$ over $\mathbb{R}^d$ given independent samples, under the assumption that $\mathbf{\Sigma}$ is graph-structured. In particular, we focus on shortest path covariance matrices, where the covariance between any two measurements is determined by the shortest path distance in an underlying graph with $d$ nodes. Such matrices generalize Toeplitz and circulant covariance matrices and are widely applied in signal processing applications, where the covariance between two measurements depends on the (shortest path) distance between them in time or space. We focus on minimizing both the vector sample complexity: the number of samples drawn from $\mathcal{D}$ and the entry sample complexity: the number of entries read in each sample. The entry sample complexity corresponds to measurement equipment costs in signal processing applications. We give a very simple algorithm for estimating $\mathbf{\Sigma}$ up to spectral norm error $\epsilon \left\|\mathbf{\Sigma}\right\|_2$ using just $O(\sqrt{D})$ entry sample complexity and $\tilde O(r^2/\epsilon^2)$ vector sample complexity, where $D$ is the diameter of the underlying graph and $r \le d$ is the rank of $\mathbf{\Sigma}$. Our method is based on extending the widely applied idea of sparse rulers for Toeplitz covariance estimation to the graph setting. In the special case when $\mathbf{\Sigma}$ is a low-rank Toeplitz matrix, our result matches the state-of-the-art, with a far simpler proof. We also give an information theoretic lower bound matching our upper bound up to a factor $D$ and discuss some directions towards closing this gap.

Distributed Newton Can Communicate Less and Resist Byzantine Workers

We develop a distributed second order optimization algorithm that is communication-efficient as well as robust against Byzantine failures of the worker machines. We propose COMRADE (COMunication-efficient and Robust Approximate Distributed nEwton), an iterative second order algorithm, where the worker machines communicate only once per iteration with the center machine. This is in sharp contrast with the state-of-the-art distributed second order algorithms like GIANT [34] and DINGO[7], where the worker machines send (functions of) local gradient and Hessian sequentially; thus ending up communicating twice with the center machine per iteration. Moreover, we show that the worker machines can further compress the local information before sending it to the center. In addition, we employ a simple norm based thresholding rule to filter-out the Byzantine worker machines. We establish the linear-quadratic rate of convergence of COMRADE and establish that the communication savings and Byzantine resilience result in only a small statistical error rate for arbitrary convex loss functions. To the best of our knowledge, this is the first work that addresses the issue of Byzantine resilience in second order distributed optimization. Furthermore, we validate our theoretical results with extensive experiments on synthetic and benchmark LIBSVM [5] data-sets and demonstrate convergence guarantees.

Communication-Efficient and Byzantine-Robust Distributed Learning

We develop a communication-efficient distributed learning algorithm that is robust against Byzantine worker machines. We propose and analyze a distributed gradient-descent algorithm that performs a simple thresholding based on gradient norms to mitigate Byzantine failures. We show the (statistical) error-rate of our algorithm matches that of [YCKB18], which uses more complicated schemes (like coordinate-wise median or trimmed mean) and thus optimal. Furthermore, for communication efficiency, we consider a generic class of {\delta}-approximate compressors from [KRSJ19] that encompasses sign-based compressors and top-k sparsification. Our algorithm uses compressed gradients and gradient norms for aggregation and Byzantine removal respectively. We establish the statistical error rate of the algorithm for arbitrary (convex or non-convex) smooth loss function. We show that, in the regime when the compression factor {\delta} is constant and the dimension of the parameter space is fixed, the rate of convergence is not affected by the compression operation, and hence we effectively get the compression for free. Moreover, we extend the compressed gradient descent algorithm with error feedback proposed in [KRSJ19] for the distributed setting. We have experimentally validated our results and shown good performance in convergence for convex (least-square regression) and non-convex (neural network training) problems.

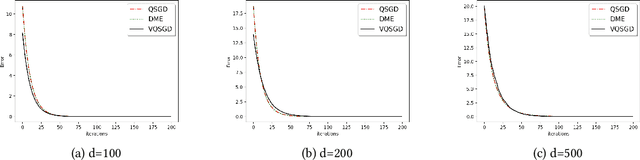
vqSGD: Vector Quantized Stochastic Gradient Descent

In this work, we present a family of vector quantization schemes vqSGD (Vector-Quantized Stochastic Gradient Descent) that provide asymptotic reduction in the communication cost with convergence guarantees in distributed computation and learning settings. In particular, we consider a randomized scheme, based on convex hull of a point set, that returns an unbiased estimator of a d-dimensional gradient vector with bounded variance. We provide multiple efficient instances of our scheme that require only O(logd) bits of communication. Further, we show that vqSGD also provides strong privacy guarantees. Experimentally, we show vqSGD performs equally well compared to other state-of-the-art quantization schemes, while substantially reducing the communication cost.

High Dimensional Discrete Integration by Hashing and Optimization

Recently Ermon et al. (2013) pioneered an ingenuous way to practically compute approximations to large scale counting or discrete integration problems by using random hashes. The hashes are used to reduce the counting problems into many separate discrete optimization problems. The optimization problems can be solved by an NP-oracle, and if they allow some amenable structure then commercial SAT solvers or linear programming (LP) solvers can be used in lieu of the NP-oracle. In particular, Ermon et al. has shown that if the domain of integration is $\{0,1\}^n$ then it is possible to obtain a $16$-approximation by this technique. In many crucial counting tasks, such as computation of partition function of ferromagnetic Potts model, the domain of integration is naturally $\{0,1,\dots, q-1\}^n, q>2$. A straightforward extension of Ermon et al.'s work would allow a $q^2$-approximation for this problem, assuming the existence of an optimization oracle. In this paper, we show that it is possible to obtain a $(2+\frac2{q-1})^2$-approximation to the discrete integration problem, when $q$ is a power of an odd prime (a similar expression follows for even $q$). We are able to achieve this by using an idea of optimization over multiple bins of the hash functions, that can be easily implemented by inequality constraints, or even in unconstrained way. Also the burden on the NP-oracle is not increased by our method (an LP solver can still be used). Furthermore, we provide a close-to-4-approximation for the permanent of a matrix by extending our technique. Note that, the domain of integration here is the symmetric group. Finally, we provide memory optimal hash functions that uses minimal number of random bits for the above purpose. We are able to obtain these structured hashes without sacrificing the amenability of the NP-oracle. We provide experimental simulation results to support our algorithms.

Robust Gradient Descent via Moment Encoding with LDPC Codes

This paper considers the problem of implementing large-scale gradient descent algorithms in a distributed computing setting in the presence of {\em straggling} processors. To mitigate the effect of the stragglers, it has been previously proposed to encode the data with an erasure-correcting code and decode at the master server at the end of the computation. We, instead, propose to encode the second-moment of the data with a low density parity-check (LDPC) code. The iterative decoding algorithms for LDPC codes have very low computational overhead and the number of decoding iterations can be made to automatically adjust with the number of stragglers in the system. We show that for a random model for stragglers, the proposed moment encoding based gradient descent method can be viewed as the stochastic gradient descent method. This allows us to obtain convergence guarantees for the proposed solution. Furthermore, the proposed moment encoding based method is shown to outperform the existing schemes in a real distributed computing setup.

Shaping Proto-Value Functions via Rewards

In this paper, we combine task-dependent reward shaping and task-independent proto-value functions to obtain reward dependent proto-value functions (RPVFs). In constructing the RPVFs we are making use of the immediate rewards which are available during the sampling phase but are not used in the PVF construction. We show via experiments that learning with an RPVF based representation is better than learning with just reward shaping or PVFs. In particular, when the state space is symmetrical and the rewards are asymmetrical, the RPVF capture the asymmetry better than the PVFs.