vqSGD: Vector Quantized Stochastic Gradient Descent

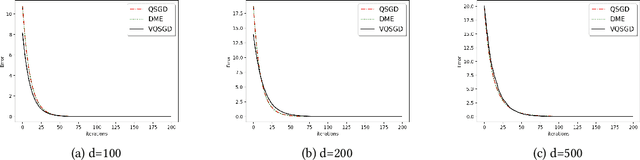
In this work, we present a family of vector quantization schemes vqSGD (Vector-Quantized Stochastic Gradient Descent) that provide asymptotic reduction in the communication cost with convergence guarantees in distributed computation and learning settings. In particular, we consider a randomized scheme, based on convex hull of a point set, that returns an unbiased estimator of a d-dimensional gradient vector with bounded variance. We provide multiple efficient instances of our scheme that require only O(logd) bits of communication. Further, we show that vqSGD also provides strong privacy guarantees. Experimentally, we show vqSGD performs equally well compared to other state-of-the-art quantization schemes, while substantially reducing the communication cost.