Optimization using Parallel Gradient Evaluations on Multiple Parameters

We propose a first-order method for convex optimization, where instead of being restricted to the gradient from a single parameter, gradients from multiple parameters can be used during each step of gradient descent. This setup is particularly useful when a few processors are available that can be used in parallel for optimization. Our method uses gradients from multiple parameters in synergy to update these parameters together towards the optima. While doing so, it is ensured that the computational and memory complexity is of the same order as that of gradient descent. Empirical results demonstrate that even using gradients from as low as \textit{two} parameters, our method can often obtain significant acceleration and provide robustness to hyper-parameter settings. We remark that the primary goal of this work is less theoretical, and is instead aimed at exploring the understudied case of using multiple gradients during each step of optimization.

Support Recovery of Sparse Signals from a Mixture of Linear Measurements

Recovery of support of a sparse vector from simple measurements is a widely studied problem, considered under the frameworks of compressed sensing, 1-bit compressed sensing, and more general single index models. We consider generalizations of this problem: mixtures of linear regressions, and mixtures of linear classifiers, where the goal is to recover supports of multiple sparse vectors using only a small number of possibly noisy linear, and 1-bit measurements respectively. The key challenge is that the measurements from different vectors are randomly mixed. Both of these problems were also extensively studied recently. In mixtures of linear classifiers, the observations correspond to the side of queried hyperplane a random unknown vector lies in, whereas in mixtures of linear regressions we observe the projection of a random unknown vector on the queried hyperplane. The primary step in recovering the unknown vectors from the mixture is to first identify the support of all the individual component vectors. In this work, we study the number of measurements sufficient for recovering the supports of all the component vectors in a mixture in both these models. We provide algorithms that use a number of measurements polynomial in $k, \log n$ and quasi-polynomial in $\ell$, to recover the support of all the $\ell$ unknown vectors in the mixture with high probability when each individual component is a $k$-sparse $n$-dimensional vector.

Recovery of sparse linear classifiers from mixture of responses

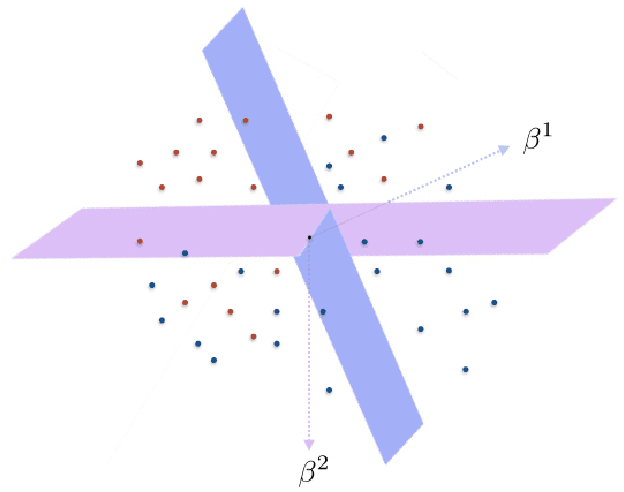
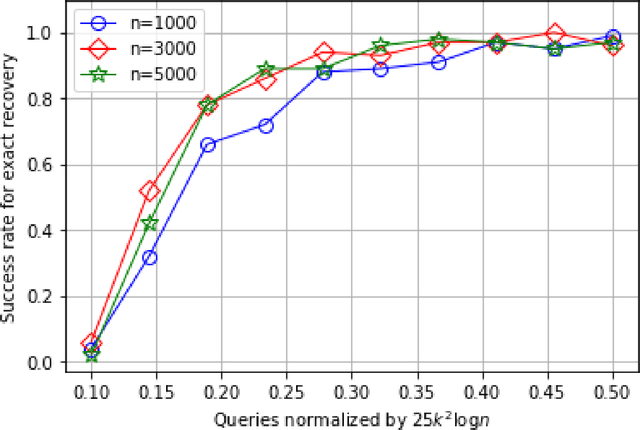
In the problem of learning a mixture of linear classifiers, the aim is to learn a collection of hyperplanes from a sequence of binary responses. Each response is a result of querying with a vector and indicates the side of a randomly chosen hyperplane from the collection the query vector belongs to. This model provides a rich representation of heterogeneous data with categorical labels and has only been studied in some special settings. We look at a hitherto unstudied problem of query complexity upper bound of recovering all the hyperplanes, especially for the case when the hyperplanes are sparse. This setting is a natural generalization of the extreme quantization problem known as 1-bit compressed sensing. Suppose we have a set of $\ell$ unknown $k$-sparse vectors. We can query the set with another vector $\boldsymbol{a}$, to obtain the sign of the inner product of $\boldsymbol{a}$ and a randomly chosen vector from the $\ell$-set. How many queries are sufficient to identify all the $\ell$ unknown vectors? This question is significantly more challenging than both the basic 1-bit compressed sensing problem (i.e., $\ell=1$ case) and the analogous regression problem (where the value instead of the sign is provided). We provide rigorous query complexity results (with efficient algorithms) for this problem.

Reliable Distributed Clustering with Redundant Data Assignment

In this paper, we present distributed generalized clustering algorithms that can handle large scale data across multiple machines in spite of straggling or unreliable machines. We propose a novel data assignment scheme that enables us to obtain global information about the entire data even when some machines fail to respond with the results of the assigned local computations. The assignment scheme leads to distributed algorithms with good approximation guarantees for a variety of clustering and dimensionality reduction problems.

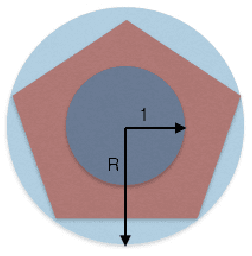
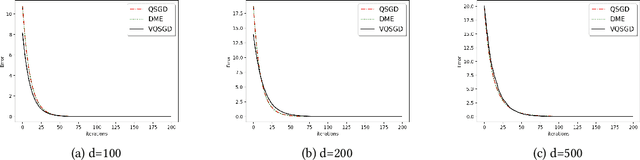
vqSGD: Vector Quantized Stochastic Gradient Descent

In this work, we present a family of vector quantization schemes vqSGD (Vector-Quantized Stochastic Gradient Descent) that provide asymptotic reduction in the communication cost with convergence guarantees in distributed computation and learning settings. In particular, we consider a randomized scheme, based on convex hull of a point set, that returns an unbiased estimator of a d-dimensional gradient vector with bounded variance. We provide multiple efficient instances of our scheme that require only O(logd) bits of communication. Further, we show that vqSGD also provides strong privacy guarantees. Experimentally, we show vqSGD performs equally well compared to other state-of-the-art quantization schemes, while substantially reducing the communication cost.