Recovery of sparse linear classifiers from mixture of responses
Paper and Code
Nov 07, 2020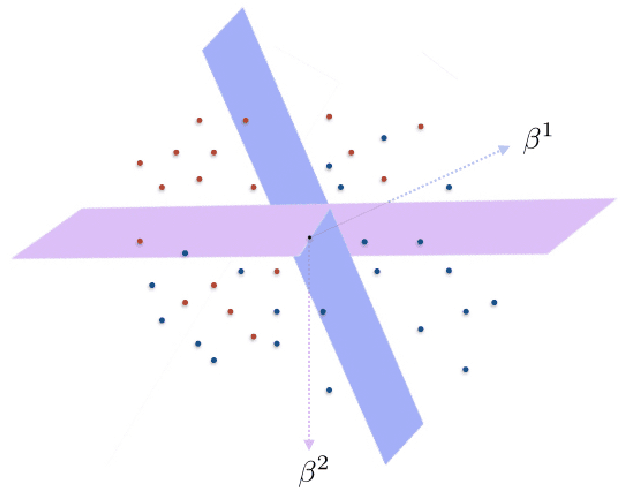
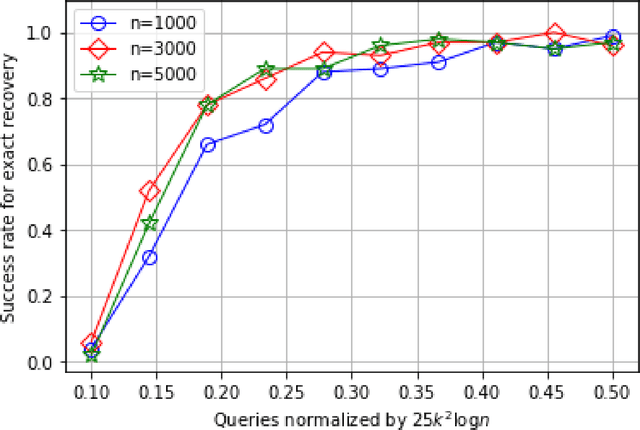
In the problem of learning a mixture of linear classifiers, the aim is to learn a collection of hyperplanes from a sequence of binary responses. Each response is a result of querying with a vector and indicates the side of a randomly chosen hyperplane from the collection the query vector belongs to. This model provides a rich representation of heterogeneous data with categorical labels and has only been studied in some special settings. We look at a hitherto unstudied problem of query complexity upper bound of recovering all the hyperplanes, especially for the case when the hyperplanes are sparse. This setting is a natural generalization of the extreme quantization problem known as 1-bit compressed sensing. Suppose we have a set of $\ell$ unknown $k$-sparse vectors. We can query the set with another vector $\boldsymbol{a}$, to obtain the sign of the inner product of $\boldsymbol{a}$ and a randomly chosen vector from the $\ell$-set. How many queries are sufficient to identify all the $\ell$ unknown vectors? This question is significantly more challenging than both the basic 1-bit compressed sensing problem (i.e., $\ell=1$ case) and the analogous regression problem (where the value instead of the sign is provided). We provide rigorous query complexity results (with efficient algorithms) for this problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge