LESS-VFL: Communication-Efficient Feature Selection for Vertical Federated Learning

We propose LESS-VFL, a communication-efficient feature selection method for distributed systems with vertically partitioned data. We consider a system of a server and several parties with local datasets that share a sample ID space but have different feature sets. The parties wish to collaboratively train a model for a prediction task. As part of the training, the parties wish to remove unimportant features in the system to improve generalization, efficiency, and explainability. In LESS-VFL, after a short pre-training period, the server optimizes its part of the global model to determine the relevant outputs from party models. This information is shared with the parties to then allow local feature selection without communication. We analytically prove that LESS-VFL removes spurious features from model training. We provide extensive empirical evidence that LESS-VFL can achieve high accuracy and remove spurious features at a fraction of the communication cost of other feature selection approaches.

Compressed-VFL: Communication-Efficient Learning with Vertically Partitioned Data

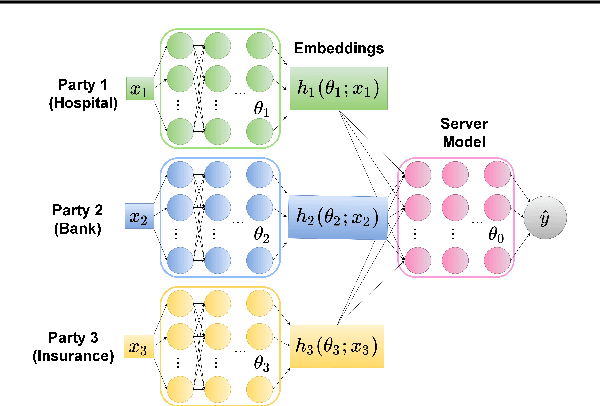
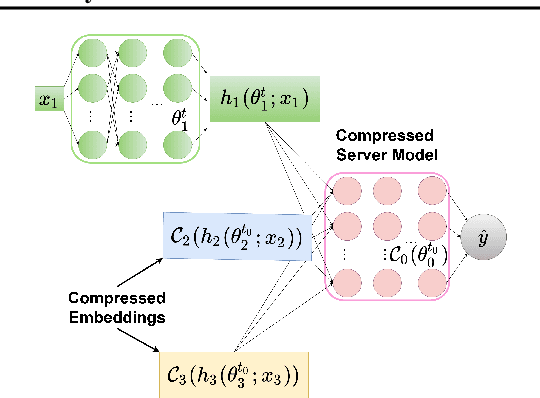
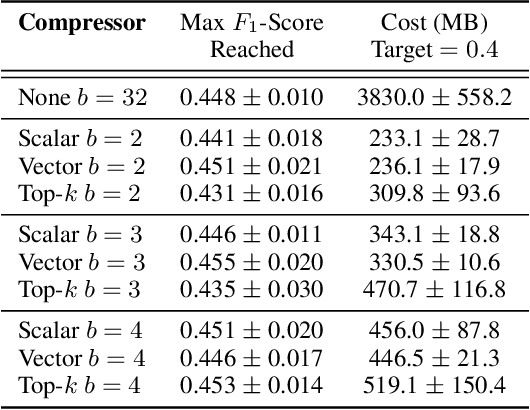
We propose Compressed Vertical Federated Learning (C-VFL) for communication-efficient training on vertically partitioned data. In C-VFL, a server and multiple parties collaboratively train a model on their respective features utilizing several local iterations and sharing compressed intermediate results periodically. Our work provides the first theoretical analysis of the effect message compression has on distributed training over vertically partitioned data. We prove convergence of non-convex objectives at a rate of $O(\frac{1}{\sqrt{T}})$ when the compression error is bounded over the course of training. We provide specific requirements for convergence with common compression techniques, such as quantization and top-$k$ sparsification. Finally, we experimentally show compression can reduce communication by over $90\%$ without a significant decrease in accuracy over VFL without compression.

Multi-Level Local SGD for Heterogeneous Hierarchical Networks

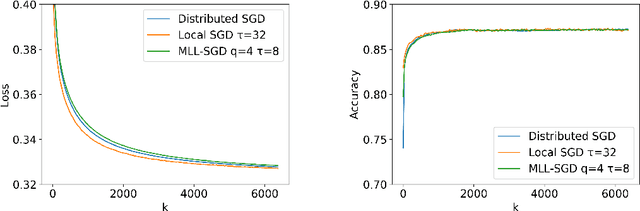
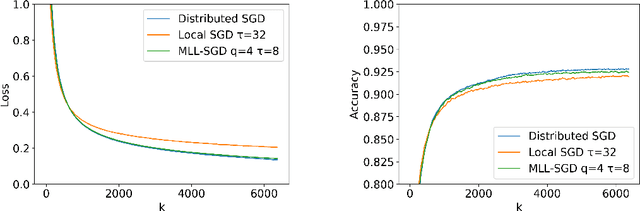
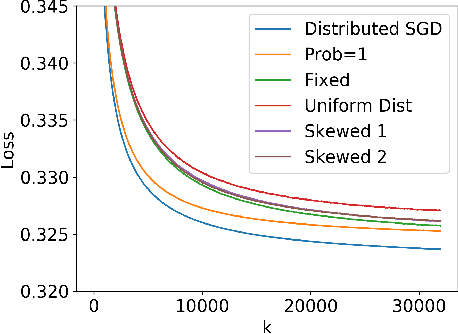
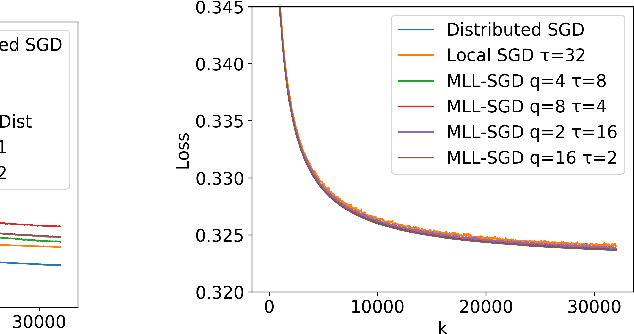
We propose Multi-Level Local SGD, a distributed gradient method for learning a smooth, non-convex objective in a heterogeneous multi-level network. Our network model consists of a set of disjoint sub-networks, with a single hub and multiple worker nodes; further, worker nodes may have different operating rates. The hubs exchange information with one another via a connected, but not necessarily complete communication network. In our algorithm, sub-networks execute a distributed SGD algorithm, using a hub-and-spoke paradigm, and the hubs periodically average their models with neighboring hubs. We first provide a unified mathematical framework that describes the Multi-Level Local SGD algorithm. We then present a theoretical analysis of the algorithm; our analysis shows the dependence of the convergence error on the worker node heterogeneity, hub network topology, and the number of local, sub-network, and global iterations. We back up our theoretical results via simulation-based experiments using both convex and non-convex objectives.