Locally Interdependent Multi-Agent MDP: Theoretical Framework for Decentralized Agents with Dynamic Dependencies
Paper and Code
Jun 10, 2024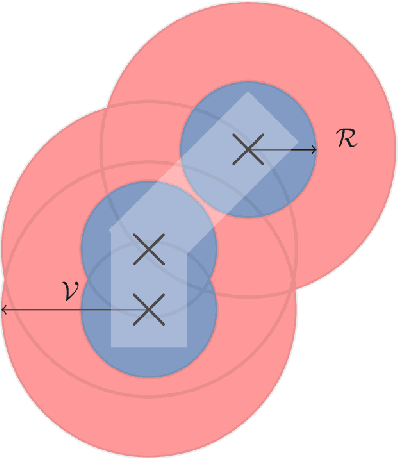
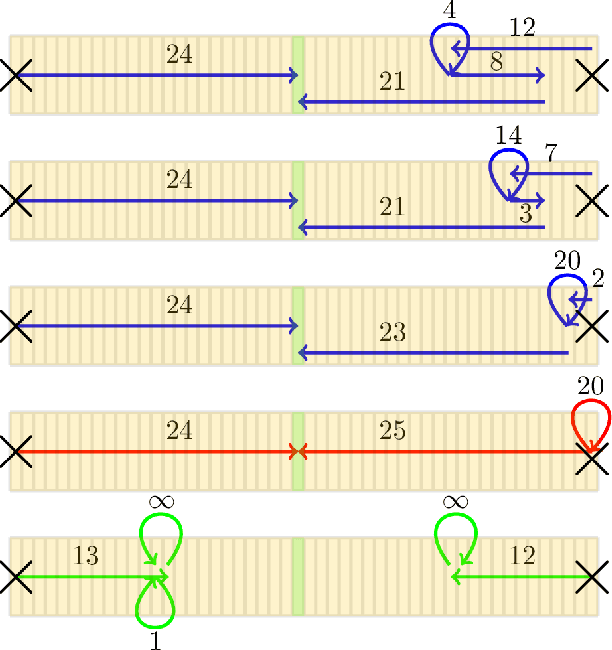
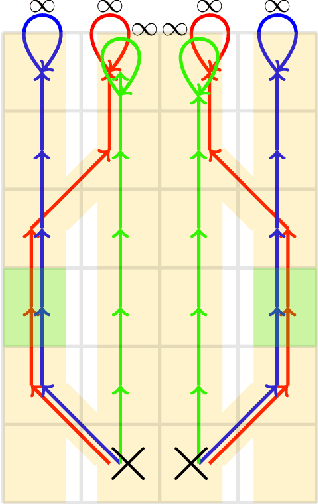
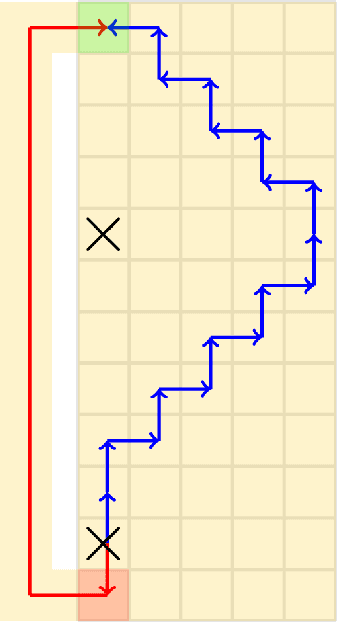
Many multi-agent systems in practice are decentralized and have dynamically varying dependencies. There has been a lack of attempts in the literature to analyze these systems theoretically. In this paper, we propose and theoretically analyze a decentralized model with dynamically varying dependencies called the Locally Interdependent Multi-Agent MDP. This model can represent problems in many disparate domains such as cooperative navigation, obstacle avoidance, and formation control. Despite the intractability that general partially observable multi-agent systems suffer from, we propose three closed-form policies that are theoretically near-optimal in this setting and can be scalable to compute and store. Consequentially, we reveal a fundamental property of Locally Interdependent Multi-Agent MDP's that the partially observable decentralized solution is exponentially close to the fully observable solution with respect to the visibility radius. We then discuss extensions of our closed-form policies to further improve tractability. We conclude by providing simulations to investigate some long horizon behaviors of our closed-form policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge