ProtiGeno: a prokaryotic short gene finder using protein language models

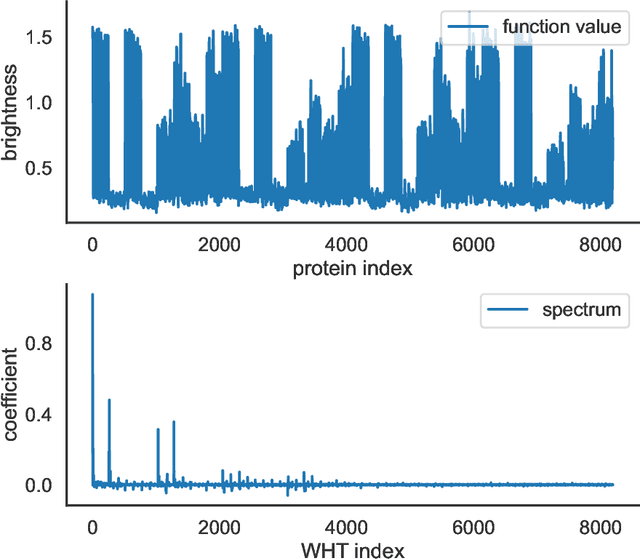
Prokaryotic gene prediction plays an important role in understanding the biology of organisms and their function with applications in medicine and biotechnology. Although the current gene finders are highly sensitive in finding long genes, their sensitivity decreases noticeably in finding shorter genes (<180 nts). The culprit is insufficient annotated gene data to identify distinguishing features in short open reading frames (ORFs). We develop a deep learning-based method called ProtiGeno, specifically targeting short prokaryotic genes using a protein language model trained on millions of evolved proteins. In systematic large-scale experiments on 4,288 prokaryotic genomes, we demonstrate that ProtiGeno predicts short coding and noncoding genes with higher accuracy and recall than the current state-of-the-art gene finders. We discuss the predictive features of ProtiGeno and possible limitations by visualizing the three-dimensional structure of the predicted short genes. Data, codes, and models are available at https://github.com/tonytu16/protigeno.

Spectral Regularization Allows Data-frugal Learning over Combinatorial Spaces

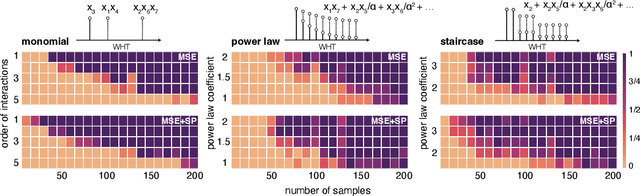
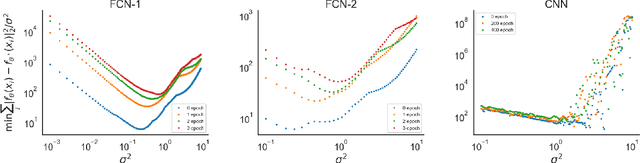
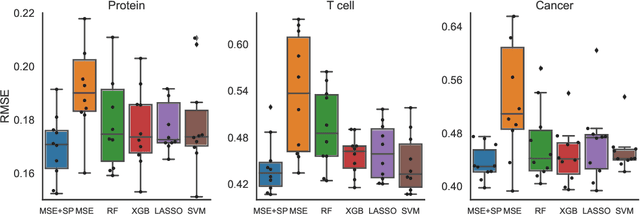
Data-driven machine learning models are being increasingly employed in several important inference problems in biology, chemistry, and physics which require learning over combinatorial spaces. Recent empirical evidence (see, e.g., [1], [2], [3]) suggests that regularizing the spectral representation of such models improves their generalization power when labeled data is scarce. However, despite these empirical studies, the theoretical underpinning of when and how spectral regularization enables improved generalization is poorly understood. In this paper, we focus on learning pseudo-Boolean functions and demonstrate that regularizing the empirical mean squared error by the L_1 norm of the spectral transform of the learned function reshapes the loss landscape and allows for data-frugal learning, under a restricted secant condition on the learner's empirical error measured against the ground truth function. Under a weaker quadratic growth condition, we show that stationary points which also approximately interpolate the training data points achieve statistically optimal generalization performance. Complementing our theory, we empirically demonstrate that running gradient descent on the regularized loss results in a better generalization performance compared to baseline algorithms in several data-scarce real-world problems.