Spencer Hutchinson
The Safety-Privacy Tradeoff in Linear Bandits
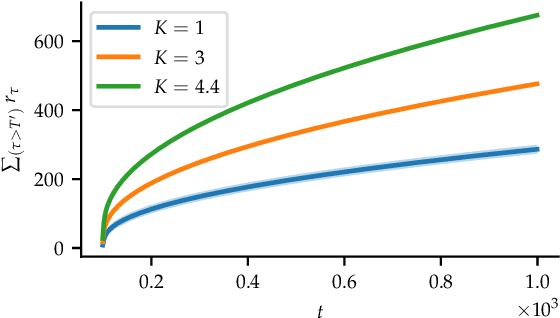
Apr 23, 2025Abstract:We consider a collection of linear stochastic bandit problems, each modeling the random response of different agents to proposed interventions, coupled together by a global safety constraint. We assume a central coordinator must choose actions to play on each bandit with the objective of regret minimization, while also ensuring that the expected response of all agents satisfies the global safety constraints at each round, in spite of uncertainty about the bandits' parameters. The agents consider their observed responses to be private and in order to protect their sensitive information, the data sharing with the central coordinator is performed under local differential privacy (LDP). However, providing higher level of privacy to different agents would have consequences in terms of safety and regret. We formalize these tradeoffs by building on the notion of the sharpness of the safety set - a measure of how the geometric properties of the safe set affects the growth of regret - and propose a unilaterally unimprovable vector of privacy levels for different agents given a maximum regret budget.
Constrained Online Convex Optimization with Polyak Feasibility Steps
Feb 18, 2025Abstract:In this work, we study online convex optimization with a fixed constraint function $g : \mathbb{R}^d \rightarrow \mathbb{R}$. Prior work on this problem has shown $O(\sqrt{T})$ regret and cumulative constraint satisfaction $\sum_{t=1}^{T} g(x_t) \leq 0$, while only accessing the constraint value and subgradient at the played actions $g(x_t), \partial g(x_t)$. Using the same constraint information, we show a stronger guarantee of anytime constraint satisfaction $g(x_t) \leq 0 \ \forall t \in [T]$, and matching $O(\sqrt{T})$ regret guarantees. These contributions are thanks to our approach of using Polyak feasibility steps to ensure constraint satisfaction, without sacrificing regret. Specifically, after each step of online gradient descent, our algorithm applies a subgradient descent step on the constraint function where the step-size is chosen according to the celebrated Polyak step-size. We further validate this approach with numerical experiments.
Safe Online Convex Optimization with Multi-Point Feedback
Jul 16, 2024
Abstract:Motivated by the stringent safety requirements that are often present in real-world applications, we study a safe online convex optimization setting where the player needs to simultaneously achieve sublinear regret and zero constraint violation while only using zero-order information. In particular, we consider a multi-point feedback setting, where the player chooses $d + 1$ points in each round (where $d$ is the problem dimension) and then receives the value of the constraint function and cost function at each of these points. To address this problem, we propose an algorithm that leverages forward-difference gradient estimation as well as optimistic and pessimistic action sets to achieve $\mathcal{O}(d \sqrt{T})$ regret and zero constraint violation under the assumption that the constraint function is smooth and strongly convex. We then perform a numerical study to investigate the impacts of the unknown constraint and zero-order feedback on empirical performance.
Optimistic Safety for Linearly-Constrained Online Convex Optimization
Mar 09, 2024Abstract:The setting of online convex optimization (OCO) under unknown constraints has garnered significant attention in recent years. In this work, we consider a version of this problem with static linear constraints that the player receives noisy feedback of and must always satisfy. By leveraging our novel design paradigm of optimistic safety, we give an algorithm for this problem that enjoys $\tilde{\mathcal{O}}(\sqrt{T})$ regret. This improves on the previous best regret bound of $\tilde{\mathcal{O}}(T^{2/3})$ while using only slightly stronger assumptions of independent noise and an oblivious adversary. Then, by recasting this problem as OCO under time-varying stochastic linear constraints, we show that our algorithm enjoys the same regret guarantees in such a setting and never violates the constraints in expectation. This contributes to the literature on OCO under time-varying stochastic constraints, where the state-of-the-art algorithms enjoy $\tilde{\mathcal{O}}(\sqrt{T})$ regret and $\tilde{\mathcal{O}}(\sqrt{T})$ violation when the constraints are convex and the player receives full feedback. Additionally, we provide a version of our algorithm that is more computationally efficient and give numerical experiments comparing it with benchmark algorithms.
Exploiting Problem Geometry in Safe Linear Bandits
Aug 29, 2023Abstract:The safe linear bandit problem is a version of the classic linear bandit problem where the learner's actions must satisfy an uncertain linear constraint at all rounds. Due its applicability to many real-world settings, this problem has received considerable attention in recent years. We find that by exploiting the geometry of the specific problem setting, we can achieve improved regret guarantees for both well-separated problem instances and action sets that are finite star convex sets. Additionally, we propose a novel algorithm for this setting that chooses problem parameters adaptively and enjoys at least as good regret guarantees as existing algorithms. Lastly, we introduce a generalization of the safe linear bandit setting where the constraints are convex and adapt our algorithms and analyses to this setting by leveraging a novel convex-analysis based approach. Simulation results show improved performance over existing algorithms for a variety of randomly sampled settings.
The Impact of the Geometric Properties of the Constraint Set in Safe Optimization with Bandit Feedback
May 01, 2023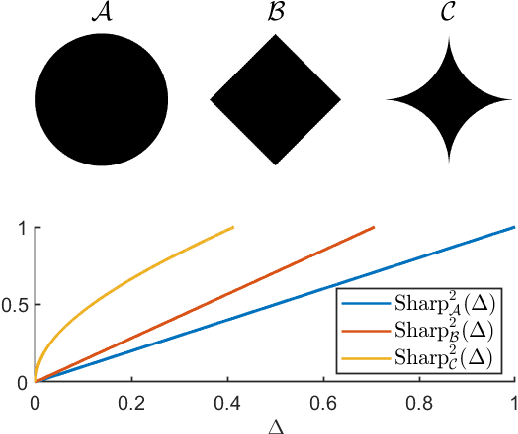
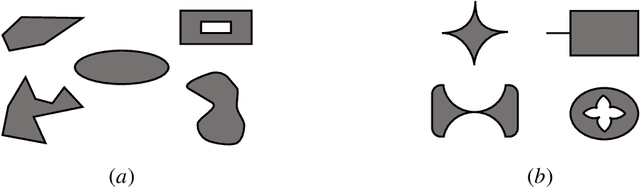
Abstract:We consider a safe optimization problem with bandit feedback in which an agent sequentially chooses actions and observes responses from the environment, with the goal of maximizing an arbitrary function of the response while respecting stage-wise constraints. We propose an algorithm for this problem, and study how the geometric properties of the constraint set impact the regret of the algorithm. In order to do so, we introduce the notion of the sharpness of a particular constraint set, which characterizes the difficulty of performing learning within the constraint set in an uncertain setting. This concept of sharpness allows us to identify the class of constraint sets for which the proposed algorithm is guaranteed to enjoy sublinear regret. Simulation results for this algorithm support the sublinear regret bound and provide empirical evidence that the sharpness of the constraint set impacts the performance of the algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge