Exploiting Problem Geometry in Safe Linear Bandits

The safe linear bandit problem is a version of the classic linear bandit problem where the learner's actions must satisfy an uncertain linear constraint at all rounds. Due its applicability to many real-world settings, this problem has received considerable attention in recent years. We find that by exploiting the geometry of the specific problem setting, we can achieve improved regret guarantees for both well-separated problem instances and action sets that are finite star convex sets. Additionally, we propose a novel algorithm for this setting that chooses problem parameters adaptively and enjoys at least as good regret guarantees as existing algorithms. Lastly, we introduce a generalization of the safe linear bandit setting where the constraints are convex and adapt our algorithms and analyses to this setting by leveraging a novel convex-analysis based approach. Simulation results show improved performance over existing algorithms for a variety of randomly sampled settings.

The Impact of the Geometric Properties of the Constraint Set in Safe Optimization with Bandit Feedback

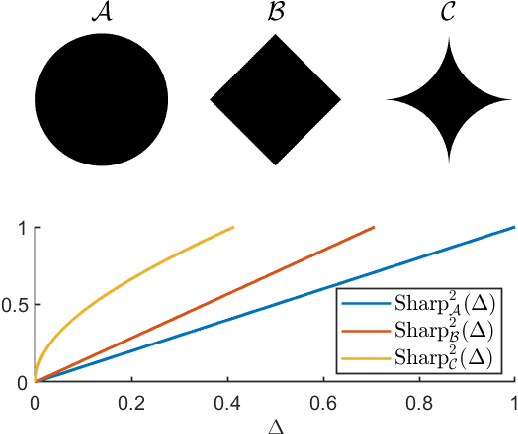
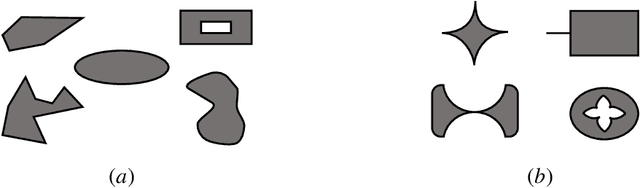
We consider a safe optimization problem with bandit feedback in which an agent sequentially chooses actions and observes responses from the environment, with the goal of maximizing an arbitrary function of the response while respecting stage-wise constraints. We propose an algorithm for this problem, and study how the geometric properties of the constraint set impact the regret of the algorithm. In order to do so, we introduce the notion of the sharpness of a particular constraint set, which characterizes the difficulty of performing learning within the constraint set in an uncertain setting. This concept of sharpness allows us to identify the class of constraint sets for which the proposed algorithm is guaranteed to enjoy sublinear regret. Simulation results for this algorithm support the sublinear regret bound and provide empirical evidence that the sharpness of the constraint set impacts the performance of the algorithm.

Robust Distributed Optimization With Randomly Corrupted Gradients

In this paper, we propose a first-order distributed optimization algorithm that is provably robust to Byzantine failures-arbitrary and potentially adversarial behavior, where all the participating agents are prone to failure. We model each agent's state over time as a two-state Markov chain that indicates Byzantine or trustworthy behaviors at different time instants. We set no restrictions on the maximum number of Byzantine agents at any given time. We design our method based on three layers of defense: 1) Temporal gradient averaging, 2) robust aggregation, and 3) gradient normalization. We study two settings for stochastic optimization, namely Sample Average Approximation and Stochastic Approximation, and prove that for strongly convex and smooth non-convex cost functions, our algorithm achieves order-optimal statistical error and convergence rates.