Robust Distributed Optimization With Randomly Corrupted Gradients

In this paper, we propose a first-order distributed optimization algorithm that is provably robust to Byzantine failures-arbitrary and potentially adversarial behavior, where all the participating agents are prone to failure. We model each agent's state over time as a two-state Markov chain that indicates Byzantine or trustworthy behaviors at different time instants. We set no restrictions on the maximum number of Byzantine agents at any given time. We design our method based on three layers of defense: 1) Temporal gradient averaging, 2) robust aggregation, and 3) gradient normalization. We study two settings for stochastic optimization, namely Sample Average Approximation and Stochastic Approximation, and prove that for strongly convex and smooth non-convex cost functions, our algorithm achieves order-optimal statistical error and convergence rates.

Communication-Efficient Distributed Cooperative Learning with Compressed Beliefs

We study the problem of distributed cooperative learning, where a group of agents seek to agree on a set of hypotheses that best describes a sequence of private observations. In the scenario where the set of hypotheses is large, we propose a belief update rule where agents share compressed (either sparse or quantized) beliefs with an arbitrary positive compression rate. Our algorithm leverages a unified and straightforward communication rule that enables agents to access wide-ranging compression operators as black-box modules. We prove the almost sure asymptotic exponential convergence of beliefs around the set of optimal hypotheses. Additionally, we show a non-asymptotic, explicit, and linear concentration rate in probability of the beliefs on the optimal hypothesis set. We provide numerical experiments to illustrate the communication benefits of our method. The simulation results show that the number of transmitted bits can be reduced to 5-10% of the non-compressed method in the studied scenarios.

A General Framework for Distributed Inference with Uncertain Models

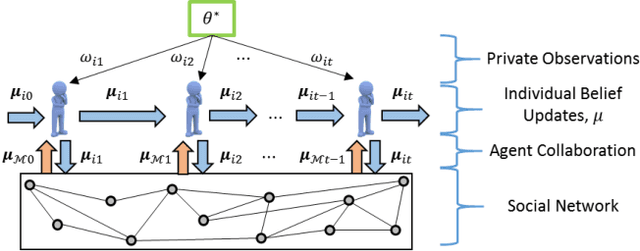
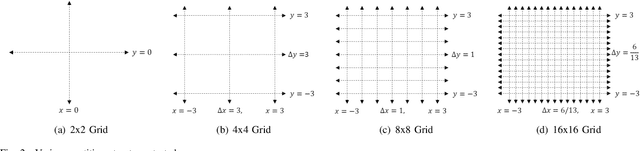
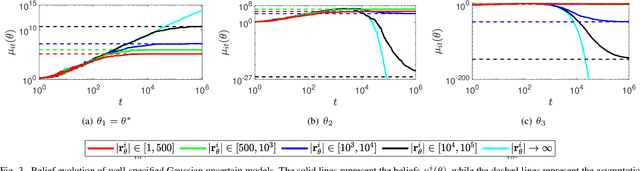
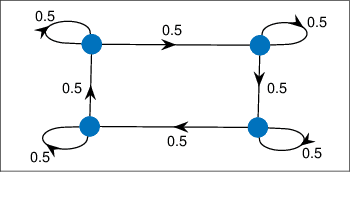
This paper studies the problem of distributed classification with a network of heterogeneous agents. The agents seek to jointly identify the underlying target class that best describes a sequence of observations. The problem is first abstracted to a hypothesis-testing framework, where we assume that the agents seek to agree on the hypothesis (target class) that best matches the distribution of observations. Non-Bayesian social learning theory provides a framework that solves this problem in an efficient manner by allowing the agents to sequentially communicate and update their beliefs for each hypothesis over the network. Most existing approaches assume that agents have access to exact statistical models for each hypothesis. However, in many practical applications, agents learn the likelihood models based on limited data, which induces uncertainty in the likelihood function parameters. In this work, we build upon the concept of uncertain models to incorporate the agents' uncertainty in the likelihoods by identifying a broad set of parametric distribution that allows the agents' beliefs to converge to the same result as a centralized approach. Furthermore, we empirically explore extensions to non-parametric models to provide a generalized framework of uncertain models in non-Bayesian social learning.

Non-Bayesian Social Learning with Uncertain Models

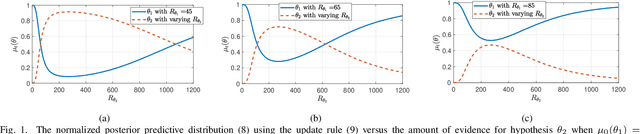
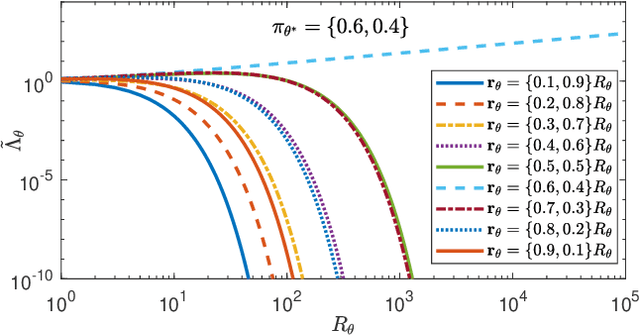
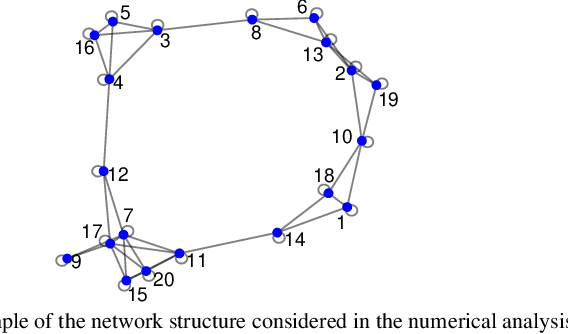
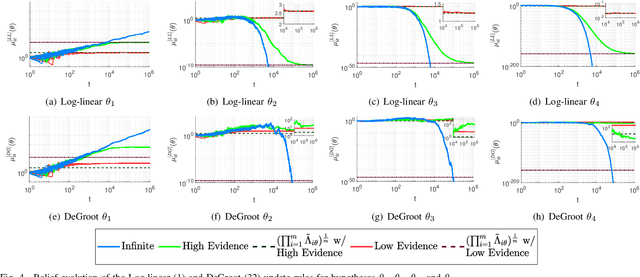
Non-Bayesian social learning theory provides a framework that models distributed inference for a group of agents interacting over a social network. In this framework, each agent iteratively forms and communicates beliefs about an unknown state of the world with their neighbors using a learning rule. Existing approaches assume agents have access to precise statistical models (in the form of likelihoods) for the state of the world. However in many situations, such models must be learned from finite data. We propose a social learning rule that takes into account uncertainty in the statistical models using second-order probabilities. Therefore, beliefs derived from uncertain models are sensitive to the amount of past evidence collected for each hypothesis. We characterize how well the hypotheses can be tested on a social network, as consistent or not with the state of the world. We explicitly show the dependency of the generated beliefs with respect to the amount of prior evidence. Moreover, as the amount of prior evidence goes to infinity, learning occurs and is consistent with traditional social learning theory.

On Curvature-aided Incremental Aggregated Gradient Methods

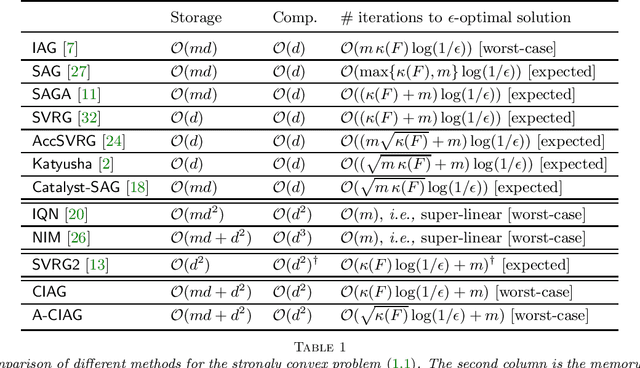
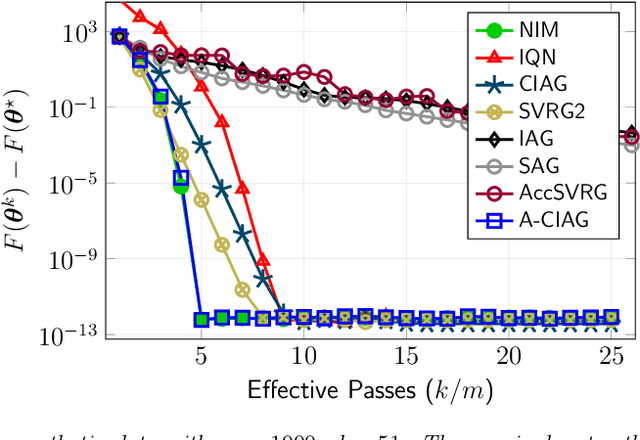
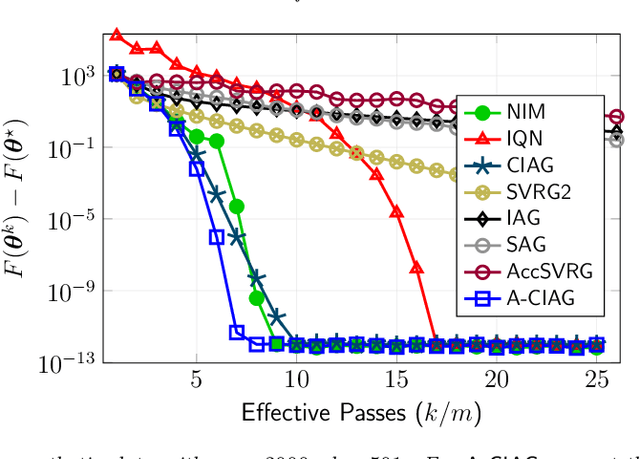
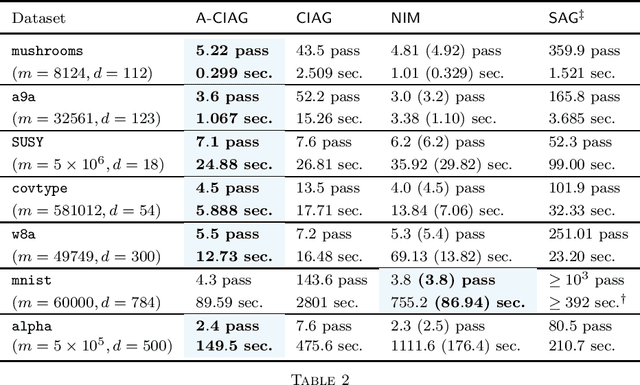
This paper studies an acceleration technique for incremental aggregated gradient methods which exploits curvature information for solving strongly convex finite sum optimization problems. These optimization problems of interest arise in large-scale learning applications relevant to machine learning systems. The proposed methods utilizes a novel curvature-aided gradient tracking technique to produce gradient estimates using the aids of Hessian information during computation. We propose and analyze two curvature-aided methods --- the first method, called curvature-aided incremental aggregated gradient (CIAG) method, can be developed from the standard gradient method and it computes an $\epsilon$-optimal solution using ${\cal O}( \kappa \log ( 1 / \epsilon ) )$ iterations for a small $\epsilon$; the second method, called accelerated CIAG (A-CIAG) method, incorporates Nesterov's acceleration into CIAG and requires ${\cal O}( \sqrt{\kappa} \log ( 1 / \epsilon ) )$ iterations for a small $\epsilon$, where $\kappa$ is the problem's condition number. Importantly, the asymptotic convergence rates above are the same as those of the full gradient and accelerated full gradient methods, respectively, and they are independent of the number of component functions involved. The proposed methods are significantly faster than the state-of-the-art methods, especially for large-scale problems with a massive amount of data. The source codes are available at https://github.com/hoitowai/ciag/