Non-Bayesian Social Learning with Uncertain Models
Paper and Code
Sep 27, 2019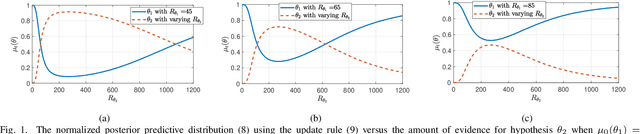
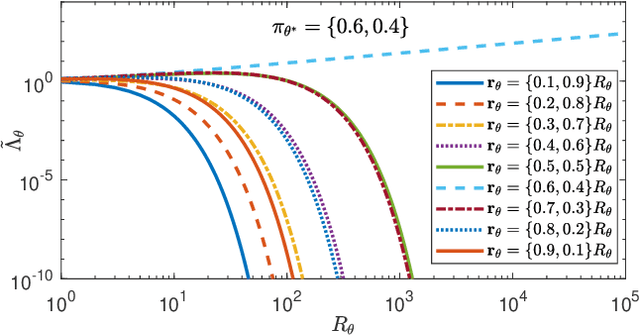
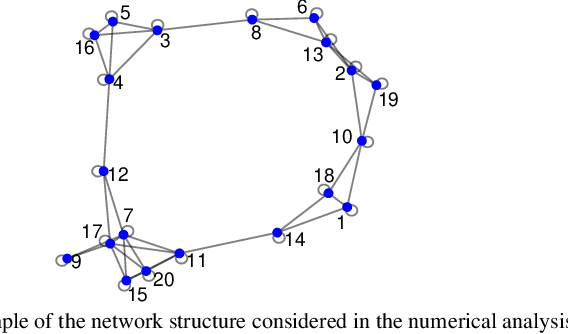
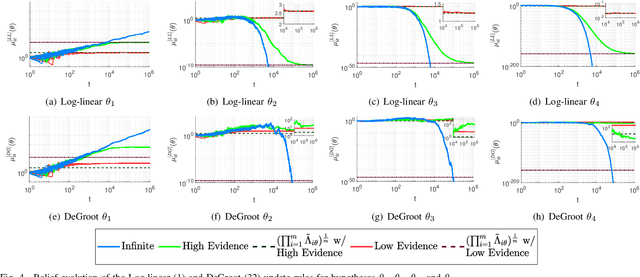
Non-Bayesian social learning theory provides a framework that models distributed inference for a group of agents interacting over a social network. In this framework, each agent iteratively forms and communicates beliefs about an unknown state of the world with their neighbors using a learning rule. Existing approaches assume agents have access to precise statistical models (in the form of likelihoods) for the state of the world. However in many situations, such models must be learned from finite data. We propose a social learning rule that takes into account uncertainty in the statistical models using second-order probabilities. Therefore, beliefs derived from uncertain models are sensitive to the amount of past evidence collected for each hypothesis. We characterize how well the hypotheses can be tested on a social network, as consistent or not with the state of the world. We explicitly show the dependency of the generated beliefs with respect to the amount of prior evidence. Moreover, as the amount of prior evidence goes to infinity, learning occurs and is consistent with traditional social learning theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge