Decentralized Federated Learning with Gradient Tracking over Time-Varying Directed Networks

We investigate the problem of agent-to-agent interaction in decentralized (federated) learning over time-varying directed graphs, and, in doing so, propose a consensus-based algorithm called DSGTm-TV. The proposed algorithm incorporates gradient tracking and heavy-ball momentum to distributively optimize a global objective function, while preserving local data privacy. Under DSGTm-TV, agents will update local model parameters and gradient estimates using information exchange with neighboring agents enabled through row- and column-stochastic mixing matrices, which we show guarantee both consensus and optimality. Our analysis establishes that DSGTm-TV exhibits linear convergence to the exact global optimum when exact gradient information is available, and converges in expectation to a neighborhood of the global optimum when employing stochastic gradients. Moreover, in contrast to existing methods, DSGTm-TV preserves convergence for networks with uncoordinated stepsizes and momentum parameters, for which we provide explicit bounds. These results enable agents to operate in a fully decentralized manner, independently optimizing their local hyper-parameters. We demonstrate the efficacy of our approach via comparisons with state-of-the-art baselines on real-world image classification and natural language processing tasks.

Support Estimation with Sampling Artifacts and Errors

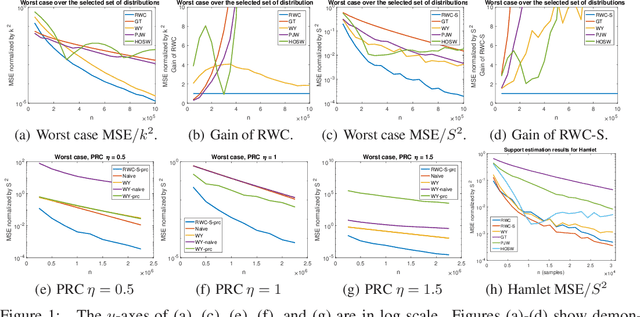
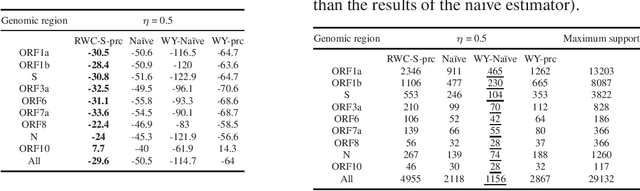
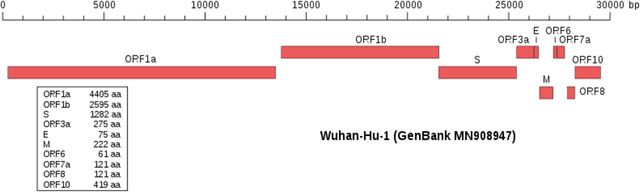
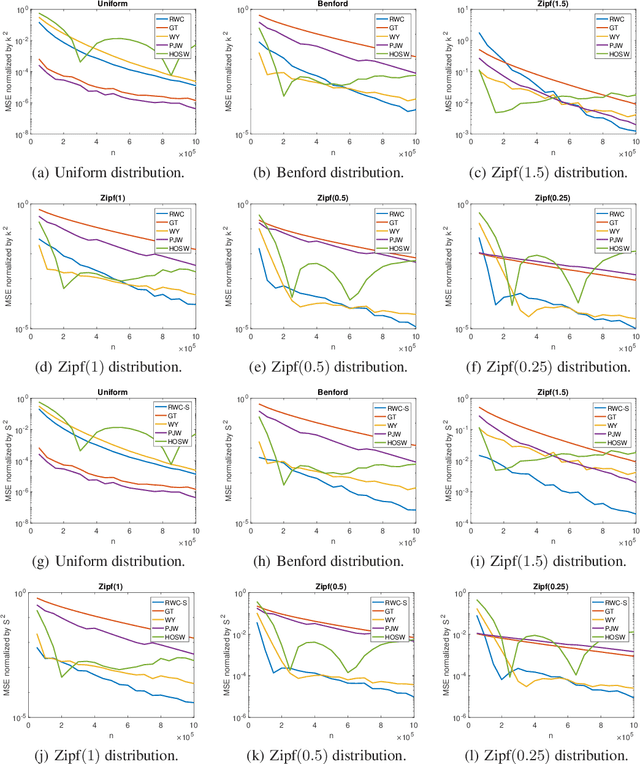
The problem of estimating the support of a distribution is of great importance in many areas of machine learning, computer science, physics and biology. Most of the existing work in this domain has focused on settings that assume perfectly accurate sampling approaches, which is seldom true in practical data science. Here we introduce the first known approach to support estimation in the presence of sampling artifacts and errors where each sample is assumed to arise from a Poisson repeat channel which simultaneously captures repetitions and deletions of samples. The proposed estimator is based on regularized weighted Chebyshev approximations, with weights governed by evaluations of so-called Touchard (Bell) polynomials. The supports in the presence of sampling artifacts are calculated using discretized semi-infite programming methods. The estimation approach is tested on synthetic and textual data, as well as on GISAID data collected to address a new problem in computational biology: mutational support estimation in genes of the SARS-Cov-2 virus. In the later setting, the Poisson channel captures the fact that many individuals are tested multiple times for the presence of viral RNA, thereby leading to repeated samples, while other individual's results are not recorded due to test errors. For all experiments performed, we observed significant improvements of our integrated methods compared to those obtained through adequate modifications of state-of-the-art noiseless support estimation methods.

On Curvature-aided Incremental Aggregated Gradient Methods

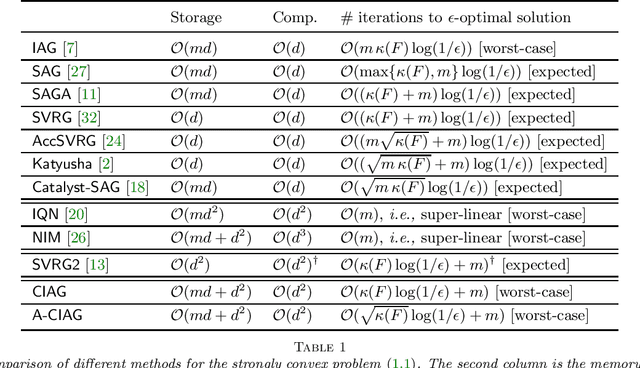
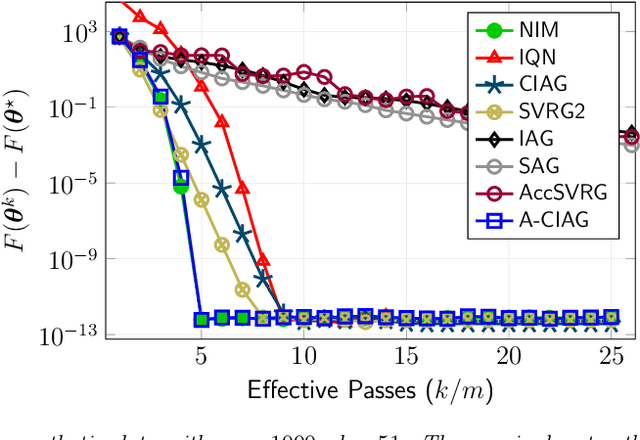
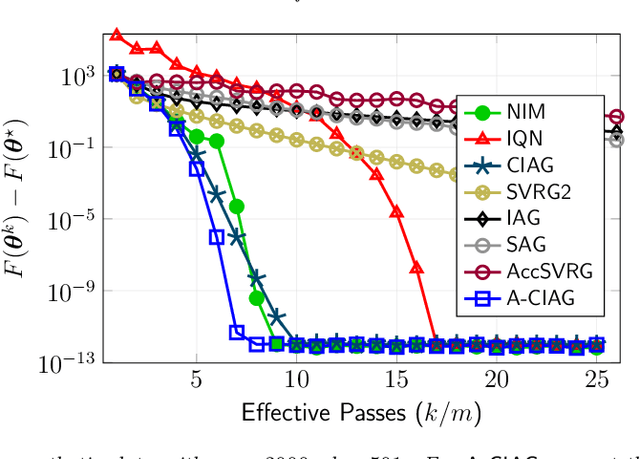
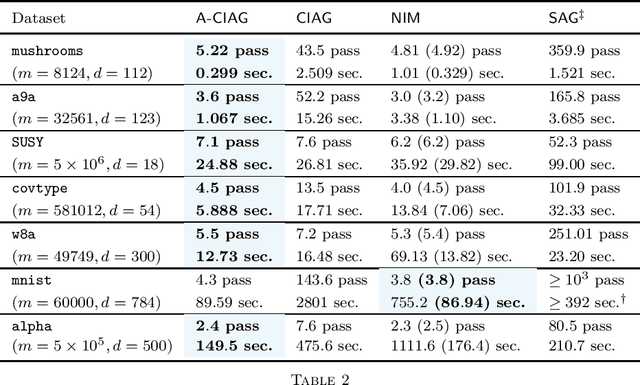
This paper studies an acceleration technique for incremental aggregated gradient methods which exploits curvature information for solving strongly convex finite sum optimization problems. These optimization problems of interest arise in large-scale learning applications relevant to machine learning systems. The proposed methods utilizes a novel curvature-aided gradient tracking technique to produce gradient estimates using the aids of Hessian information during computation. We propose and analyze two curvature-aided methods --- the first method, called curvature-aided incremental aggregated gradient (CIAG) method, can be developed from the standard gradient method and it computes an $\epsilon$-optimal solution using ${\cal O}( \kappa \log ( 1 / \epsilon ) )$ iterations for a small $\epsilon$; the second method, called accelerated CIAG (A-CIAG) method, incorporates Nesterov's acceleration into CIAG and requires ${\cal O}( \sqrt{\kappa} \log ( 1 / \epsilon ) )$ iterations for a small $\epsilon$, where $\kappa$ is the problem's condition number. Importantly, the asymptotic convergence rates above are the same as those of the full gradient and accelerated full gradient methods, respectively, and they are independent of the number of component functions involved. The proposed methods are significantly faster than the state-of-the-art methods, especially for large-scale problems with a massive amount of data. The source codes are available at https://github.com/hoitowai/ciag/