Preserving Smart Grid Integrity: A Differential Privacy Framework for Secure Detection of False Data Injection Attacks in the Smart Grid

In this paper, we present a framework based on differential privacy (DP) for querying electric power measurements to detect system anomalies or bad data caused by false data injections (FDIs). Our DP approach conceals consumption and system matrix data, while simultaneously enabling an untrusted third party to test hypotheses of anomalies, such as an FDI attack, by releasing a randomized sufficient statistic for hypothesis-testing. We consider a measurement model corrupted by Gaussian noise and a sparse noise vector representing the attack, and we observe that the optimal test statistic is a chi-square random variable. To detect possible attacks, we propose a novel DP chi-square noise mechanism that ensures the test does not reveal private information about power injections or the system matrix. The proposed framework provides a robust solution for detecting FDIs while preserving the privacy of sensitive power system data.

MALCOM-PSGD: Inexact Proximal Stochastic Gradient Descent for Communication-Efficient Decentralized Machine Learning

Recent research indicates that frequent model communication stands as a major bottleneck to the efficiency of decentralized machine learning (ML), particularly for large-scale and over-parameterized neural networks (NNs). In this paper, we introduce MALCOM-PSGD, a new decentralized ML algorithm that strategically integrates gradient compression techniques with model sparsification. MALCOM-PSGD leverages proximal stochastic gradient descent to handle the non-smoothness resulting from the $\ell_1$ regularization in model sparsification. Furthermore, we adapt vector source coding and dithering-based quantization for compressed gradient communication of sparsified models. Our analysis shows that decentralized proximal stochastic gradient descent with compressed communication has a convergence rate of $\mathcal{O}\left(\ln(t)/\sqrt{t}\right)$ assuming a diminishing learning rate and where $t$ denotes the number of iterations. Numerical results verify our theoretical findings and demonstrate that our method reduces communication costs by approximately $75\%$ when compared to the state-of-the-art method.

Blind Graph Matching Using Graph Signals

Classical graph matching aims to find a node correspondence between two unlabeled graphs of known topologies. This problem has a wide range of applications, from matching identities in social networks to identifying similar biological network functions across species. However, when the underlying graphs are unknown, the use of conventional graph matching methods requires inferring the graph topologies first, a process that is highly sensitive to observation errors. In this paper, we tackle the blind graph matching problem with unknown underlying graphs directly using observations of graph signals, which are generated from graph filters applied to graph signal excitations. We propose to construct sample covariance matrices from the observed signals and match the nodes based on the selected sample eigenvectors. Our analysis shows that the blind matching outcome converges to the result obtained with known graph topologies when the signal sampling size is large and the signal noise is small. Numerical results showcase the performance improvement of the proposed algorithm compared to matching two estimated underlying graphs learned from the graph signals.

Differential Privacy for Class-based Data: A Practical Gaussian Mechanism

In this paper, we present a notion of differential privacy (DP) for data that comes from different classes. Here, the class-membership is private information that needs to be protected. The proposed method is an output perturbation mechanism that adds noise to the release of query response such that the analyst is unable to infer the underlying class-label. The proposed DP method is capable of not only protecting the privacy of class-based data but also meets quality metrics of accuracy and is computationally efficient and practical. We illustrate the efficacy of the proposed method empirically while outperforming the baseline additive Gaussian noise mechanism. We also examine a real-world application and apply the proposed DP method to the autoregression and moving average (ARMA) forecasting method, protecting the privacy of the underlying data source. Case studies on the real-world advanced metering infrastructure (AMI) measurements of household power consumption validate the excellent performance of the proposed DP method while also satisfying the accuracy of forecasted power consumption measurements.

Solar Photovoltaic Systems Metadata Inference and Differentially Private Publication

Stakeholders in electricity delivery infrastructure are amassing data about their system demand, use, and operations. Still, they are reluctant to share them, as even sharing aggregated or anonymized electric grid data risks the disclosure of sensitive information. This paper highlights how applying differential privacy to distributed energy resource production data can preserve the usefulness of that data for operations, planning, and research purposes without violating privacy constraints. Differentially private mechanisms can be optimized for queries of interest in the energy sector, with provable privacy and accuracy trade-offs, and can help design differentially private databases for further analysis and research. In this paper, we consider the problem of inference and publication of solar photovoltaic systems' metadata. Metadata such as nameplate capacity, surface azimuth and surface tilt may reveal personally identifiable information regarding the installation behind-the-meter. We describe a methodology to infer the metadata and propose a mechanism based on Bayesian optimization to publish the inferred metadata in a differentially private manner. The proposed mechanism is numerically validated using real-world solar power generation data.

Complex-Value Spatio-temporal Graph Convolutional Neural Networks and its Applications to Electric Power Systems AI

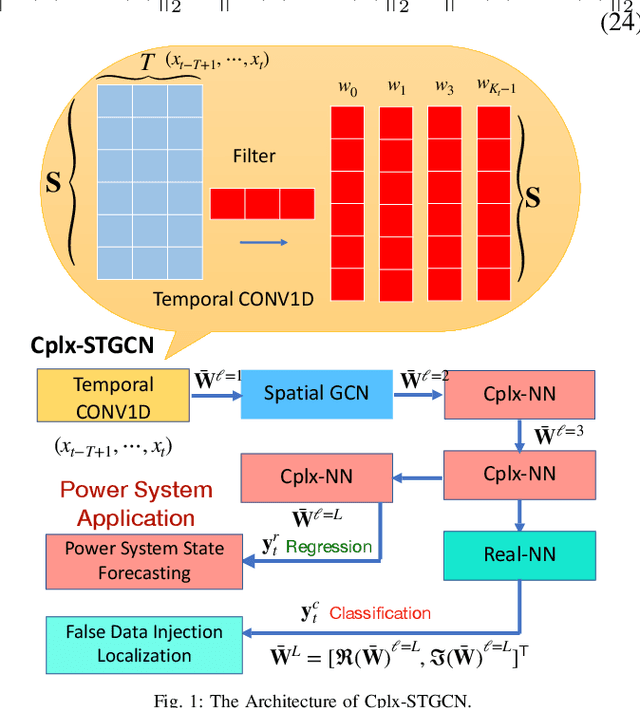
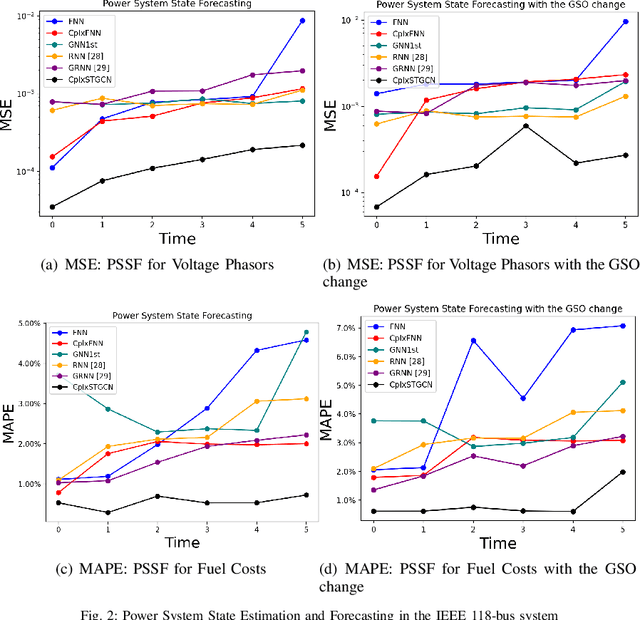
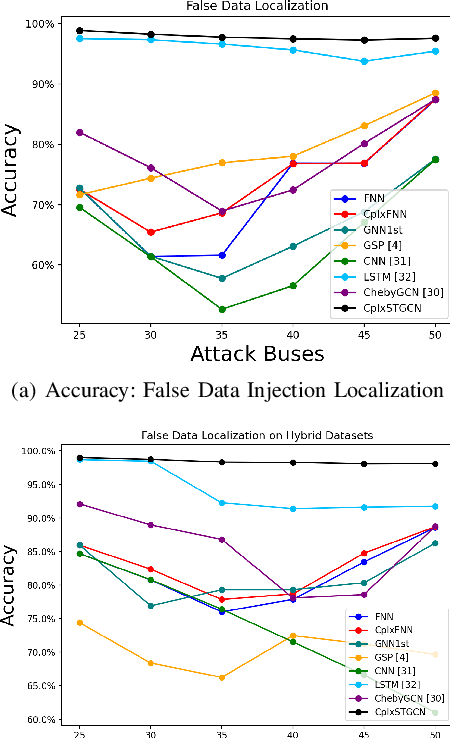
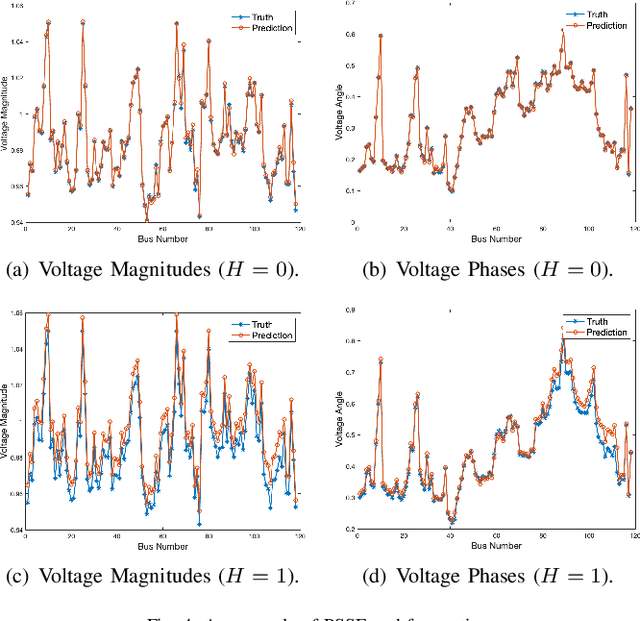
The effective representation, precessing, analysis, and visualization of large-scale structured data over graphs are gaining a lot of attention. So far most of the literature has focused on real-valued signals. However, signals are often sparse in the Fourier domain, and more informative and compact representations for them can be obtained using the complex envelope of their spectral components, as opposed to the original real-valued signals. Motivated by this fact, in this work we generalize graph convolutional neural networks (GCN) to the complex domain, deriving the theory that allows to incorporate a complex-valued graph shift operators (GSO) in the definition of graph filters (GF) and process complex-valued graph signals (GS). The theory developed can handle spatio-temporal complex network processes. We prove that complex-valued GCNs are stable with respect to perturbations of the underlying graph support, the bound of the transfer error and the bound of error propagation through multiply layers. Then we apply complex GCN to power grid state forecasting, power grid cyber-attack detection and localization.

Differentially Private $K$-means Clustering Applied to Meter Data Analysis and Synthesis

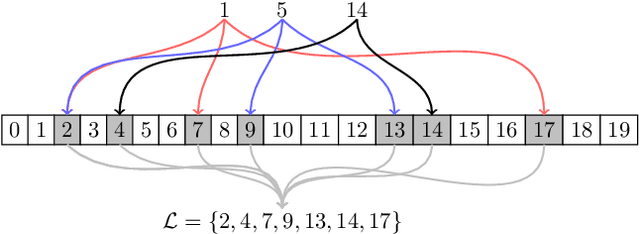
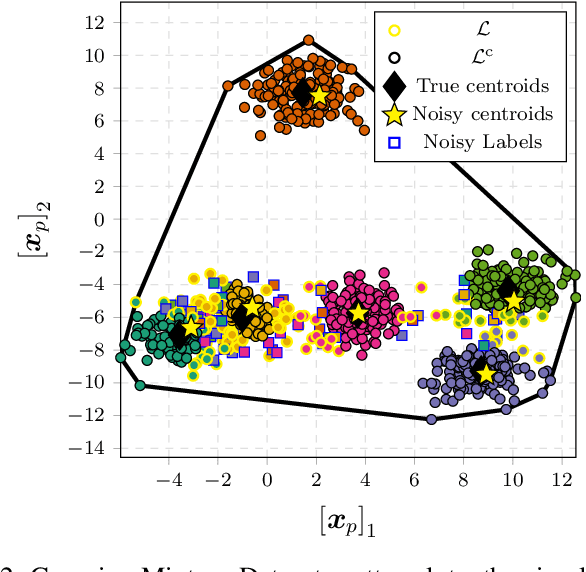
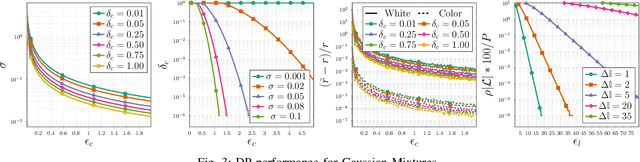
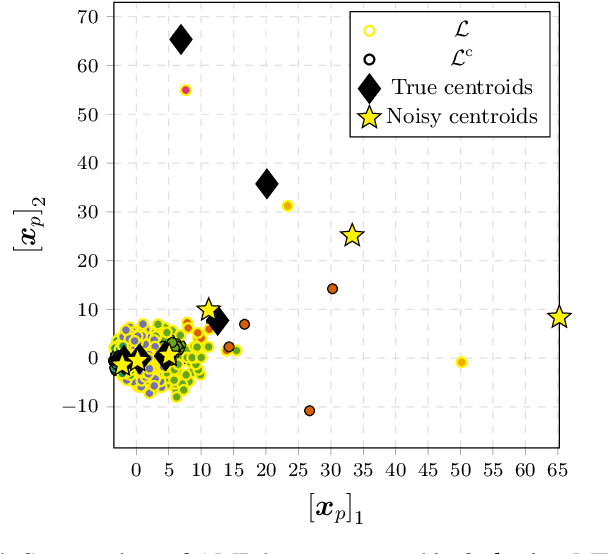
The proliferation of smart meters has resulted in a large amount of data being generated. It is increasingly apparent that methods are required for allowing a variety of stakeholders to leverage the data in a manner that preserves the privacy of the consumers. The sector is scrambling to define policies, such as the so called '15/15 rule', to respond to the need. However, the current policies fail to adequately guarantee privacy. In this paper, we address the problem of allowing third parties to apply $K$-means clustering, obtaining customer labels and centroids for a set of load time series by applying the framework of differential privacy. We leverage the method to design an algorithm that generates differentially private synthetic load data consistent with the labeled data. We test our algorithm's utility by answering summary statistics such as average daily load profiles for a 2-dimensional synthetic dataset and a real-world power load dataset.

Colored Noise Mechanism for Differentially Private Clustering

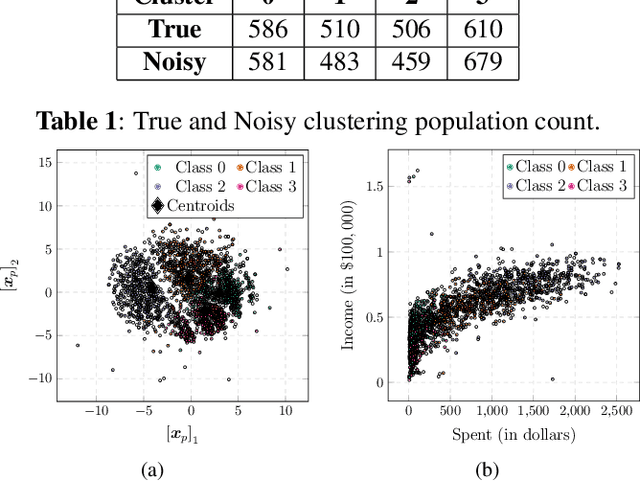
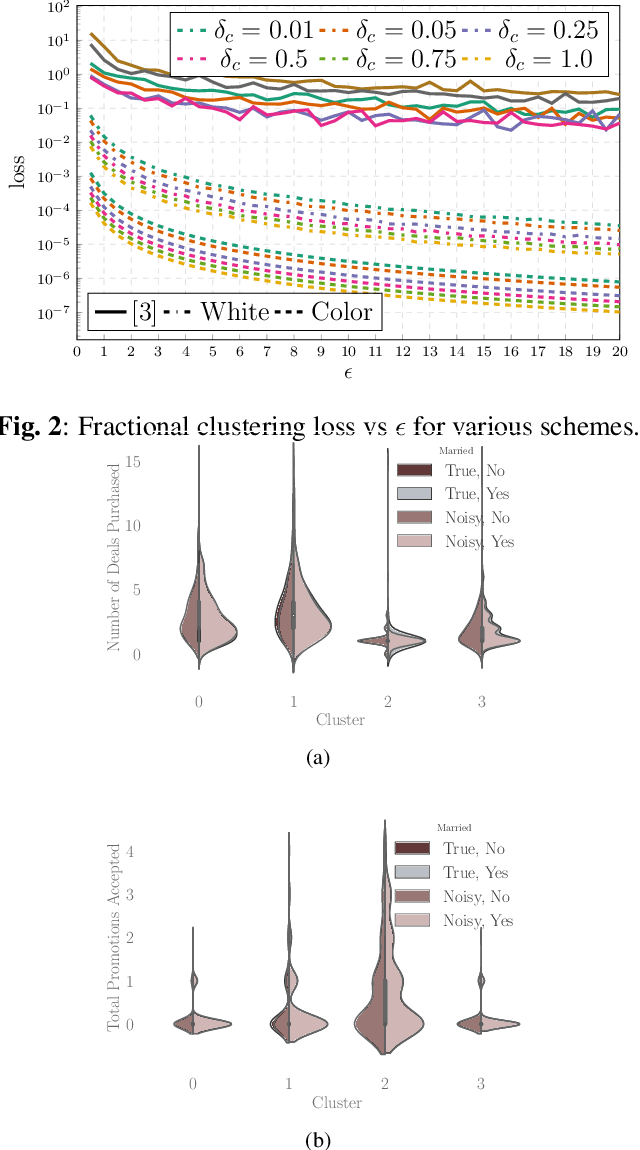
The goal of this paper is to propose and analyze a differentially private randomized mechanism for the $K$-means query. The goal is to ensure that the information received about the cluster-centroids is differentially private. The method consists in adding Gaussian noise with an optimum covariance. The main result of the paper is the analytical solution for the optimum covariance as a function of the database. Comparisons with the state of the art prove the efficacy of our approach.

Grid-Graph Signal Processing : A Graph Signal Processing Framework for the Power Grid

The underlying theme of this paper is to explore the various facets of power systems data through the lens of graph signal processing (GSP), laying down the foundations of the Grid-GSP framework. Grid-GSP provides an interpretation for the spatio-temporal properties of voltage phasor measurements, by showing how the well-known power systems modeling supports a generative low-pass graph filter model for the state variables, namely the voltage phasors. Using the model we formalize the empirical observation that voltage phasor measurement data lie in a low-dimensional subspace and tie their spatio-temporal structure to generator voltage dynamics. The Grid-GSP generative model is then successfully employed to investigate the problems pertaining to the grid of data sampling and interpolation, network inference, detection of anomalies and data compression. Numerical results on a large synthetic grid that mimics the real-grid of the state of Texas, ACTIVSg2000, and on real-world measurements from ISO-New England verify the efficacy of applying Grid-GSP methods to electric grid data.

A User Guide to Low-Pass Graph Signal Processing and its Applications

The notion of graph filters can be used to define generative models for graph data. In fact, the data obtained from many examples of network dynamics may be viewed as the output of a graph filter. With this interpretation, classical signal processing tools such as frequency analysis have been successfully applied with analogous interpretation to graph data, generating new insights for data science. What follows is a user guide on a specific class of graph data, where the generating graph filters are low-pass, i.e., the filter attenuates contents in the higher graph frequencies while retaining contents in the lower frequencies. Our choice is motivated by the prevalence of low-pass models in application domains such as social networks, financial markets, and power systems. We illustrate how to leverage properties of low-pass graph filters to learn the graph topology or identify its community structure; efficiently represent graph data through sampling, recover missing measurements, and de-noise graph data; the low-pass property is also used as the baseline to detect anomalies.