Differential Privacy for Class-based Data: A Practical Gaussian Mechanism

In this paper, we present a notion of differential privacy (DP) for data that comes from different classes. Here, the class-membership is private information that needs to be protected. The proposed method is an output perturbation mechanism that adds noise to the release of query response such that the analyst is unable to infer the underlying class-label. The proposed DP method is capable of not only protecting the privacy of class-based data but also meets quality metrics of accuracy and is computationally efficient and practical. We illustrate the efficacy of the proposed method empirically while outperforming the baseline additive Gaussian noise mechanism. We also examine a real-world application and apply the proposed DP method to the autoregression and moving average (ARMA) forecasting method, protecting the privacy of the underlying data source. Case studies on the real-world advanced metering infrastructure (AMI) measurements of household power consumption validate the excellent performance of the proposed DP method while also satisfying the accuracy of forecasted power consumption measurements.

Inferring Class Label Distribution of Training Data from Classifiers: An Accuracy-Augmented Meta-Classifier Attack

Property inference attacks against machine learning (ML) models aim to infer properties of the training data that are unrelated to the primary task of the model, and have so far been formulated as binary decision problems, i.e., whether or not the training data have a certain property. However, in industrial and healthcare applications, the proportion of labels in the training data is quite often also considered sensitive information. In this paper we introduce a new type of property inference attack that unlike binary decision problems in literature, aim at inferring the class label distribution of the training data from parameters of ML classifier models. We propose a method based on \emph{shadow training} and a \emph{meta-classifier} trained on the parameters of the shadow classifiers augmented with the accuracy of the classifiers on auxiliary data. We evaluate the proposed approach for ML classifiers with fully connected neural network architectures. We find that the proposed \emph{meta-classifier} attack provides a maximum relative improvement of $52\%$ over state of the art.

Grid-Graph Signal Processing : A Graph Signal Processing Framework for the Power Grid

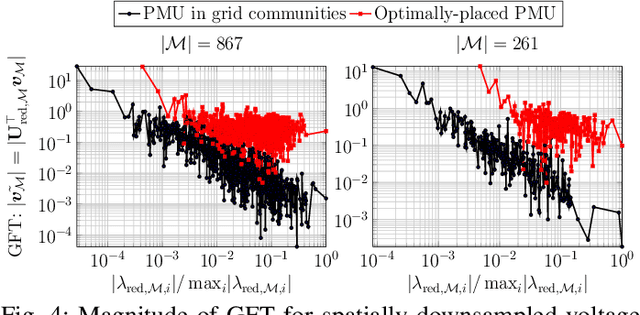
The underlying theme of this paper is to explore the various facets of power systems data through the lens of graph signal processing (GSP), laying down the foundations of the Grid-GSP framework. Grid-GSP provides an interpretation for the spatio-temporal properties of voltage phasor measurements, by showing how the well-known power systems modeling supports a generative low-pass graph filter model for the state variables, namely the voltage phasors. Using the model we formalize the empirical observation that voltage phasor measurement data lie in a low-dimensional subspace and tie their spatio-temporal structure to generator voltage dynamics. The Grid-GSP generative model is then successfully employed to investigate the problems pertaining to the grid of data sampling and interpolation, network inference, detection of anomalies and data compression. Numerical results on a large synthetic grid that mimics the real-grid of the state of Texas, ACTIVSg2000, and on real-world measurements from ISO-New England verify the efficacy of applying Grid-GSP methods to electric grid data.

A User Guide to Low-Pass Graph Signal Processing and its Applications

The notion of graph filters can be used to define generative models for graph data. In fact, the data obtained from many examples of network dynamics may be viewed as the output of a graph filter. With this interpretation, classical signal processing tools such as frequency analysis have been successfully applied with analogous interpretation to graph data, generating new insights for data science. What follows is a user guide on a specific class of graph data, where the generating graph filters are low-pass, i.e., the filter attenuates contents in the higher graph frequencies while retaining contents in the lower frequencies. Our choice is motivated by the prevalence of low-pass models in application domains such as social networks, financial markets, and power systems. We illustrate how to leverage properties of low-pass graph filters to learn the graph topology or identify its community structure; efficiently represent graph data through sampling, recover missing measurements, and de-noise graph data; the low-pass property is also used as the baseline to detect anomalies.