Complex-Value Spatio-temporal Graph Convolutional Neural Networks and its Applications to Electric Power Systems AI

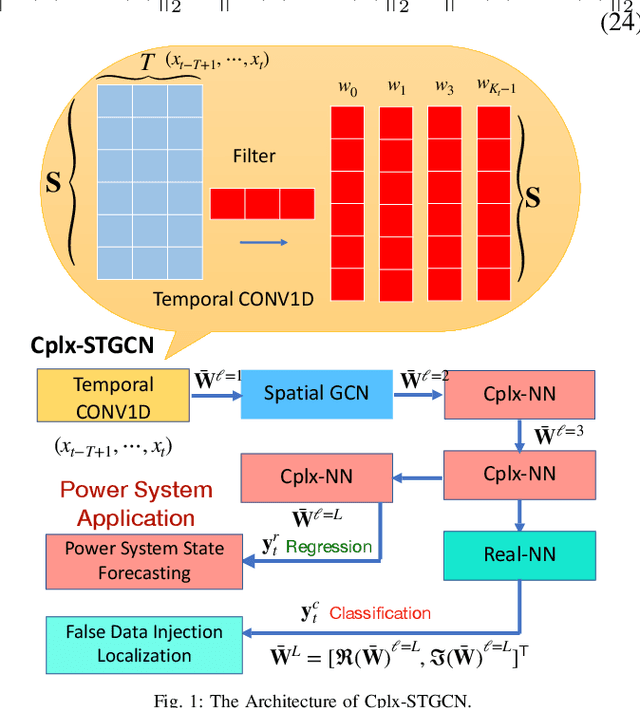
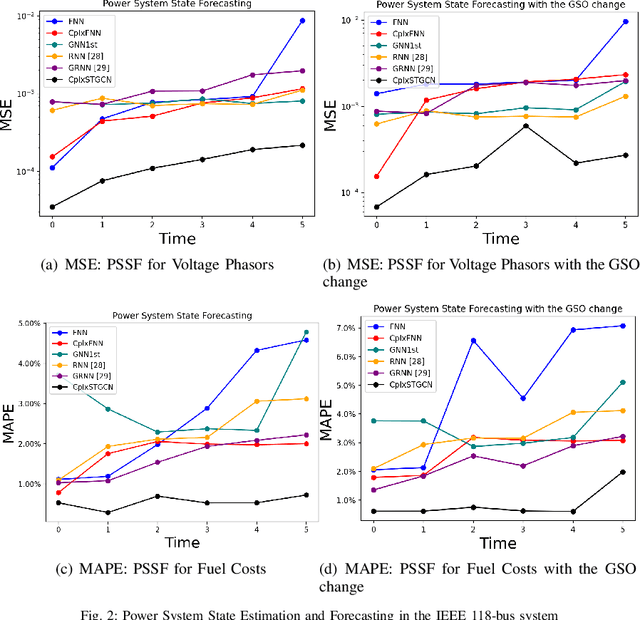
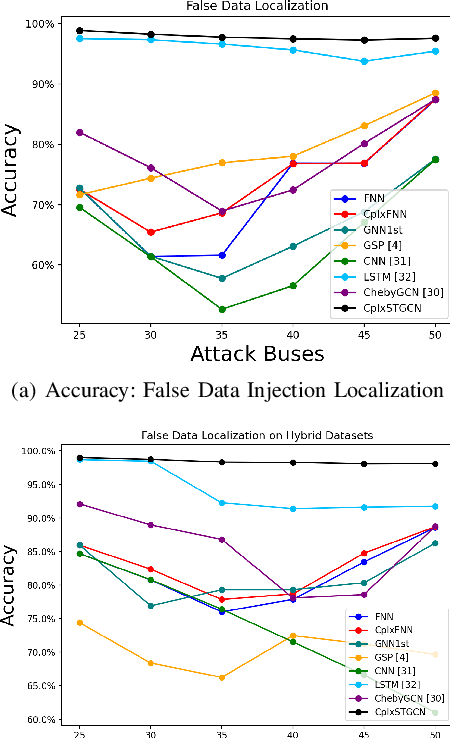
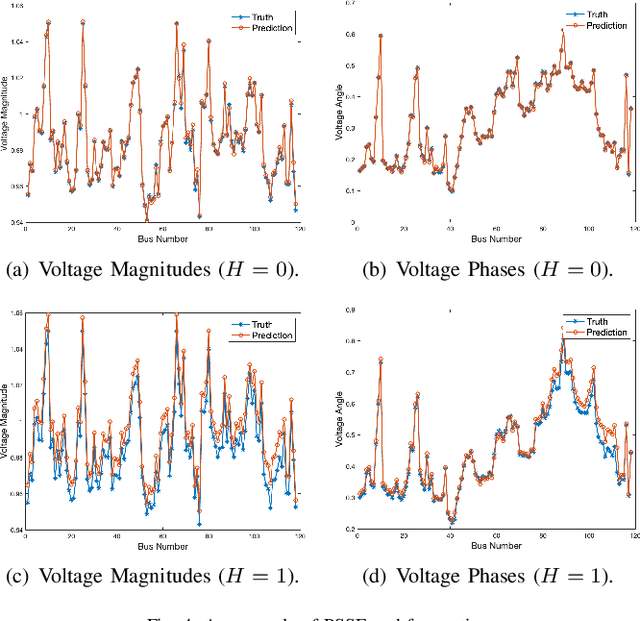
The effective representation, precessing, analysis, and visualization of large-scale structured data over graphs are gaining a lot of attention. So far most of the literature has focused on real-valued signals. However, signals are often sparse in the Fourier domain, and more informative and compact representations for them can be obtained using the complex envelope of their spectral components, as opposed to the original real-valued signals. Motivated by this fact, in this work we generalize graph convolutional neural networks (GCN) to the complex domain, deriving the theory that allows to incorporate a complex-valued graph shift operators (GSO) in the definition of graph filters (GF) and process complex-valued graph signals (GS). The theory developed can handle spatio-temporal complex network processes. We prove that complex-valued GCNs are stable with respect to perturbations of the underlying graph support, the bound of the transfer error and the bound of error propagation through multiply layers. Then we apply complex GCN to power grid state forecasting, power grid cyber-attack detection and localization.

Learning from learning machines: a new generation of AI technology to meet the needs of science

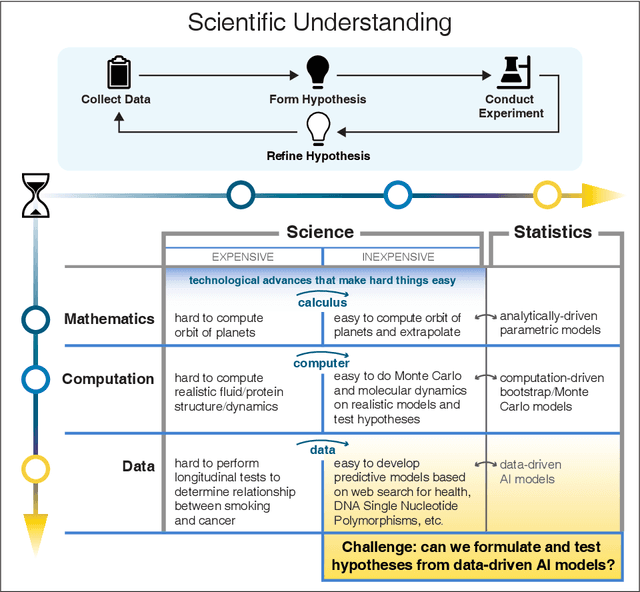
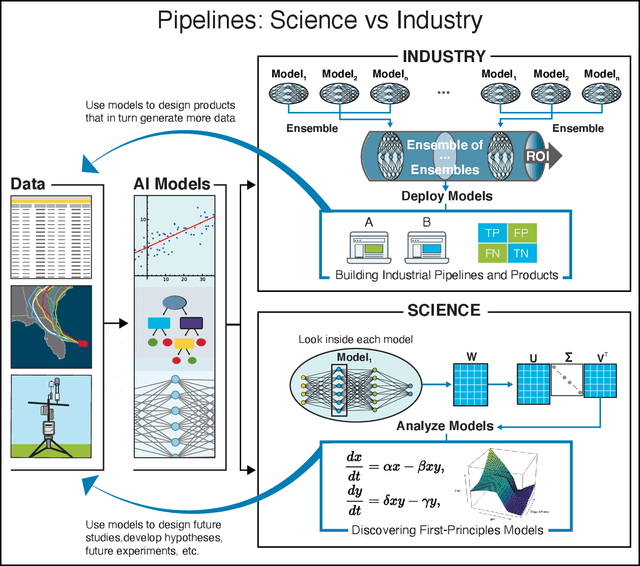
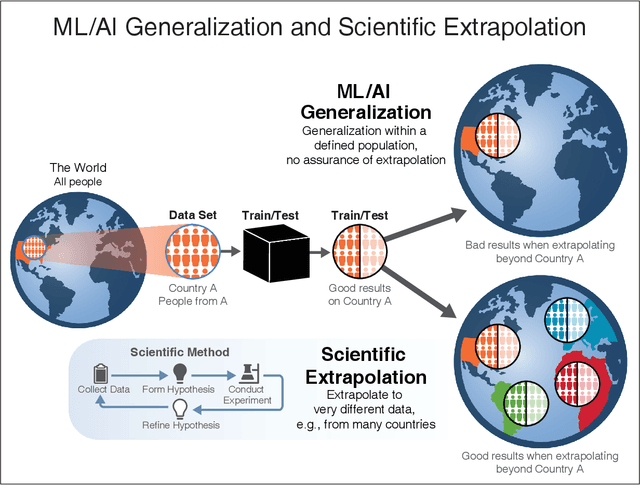
We outline emerging opportunities and challenges to enhance the utility of AI for scientific discovery. The distinct goals of AI for industry versus the goals of AI for science create tension between identifying patterns in data versus discovering patterns in the world from data. If we address the fundamental challenges associated with "bridging the gap" between domain-driven scientific models and data-driven AI learning machines, then we expect that these AI models can transform hypothesis generation, scientific discovery, and the scientific process itself.

Regression-based Inverter Control for Decentralized Optimal Power Flow and Voltage Regulation

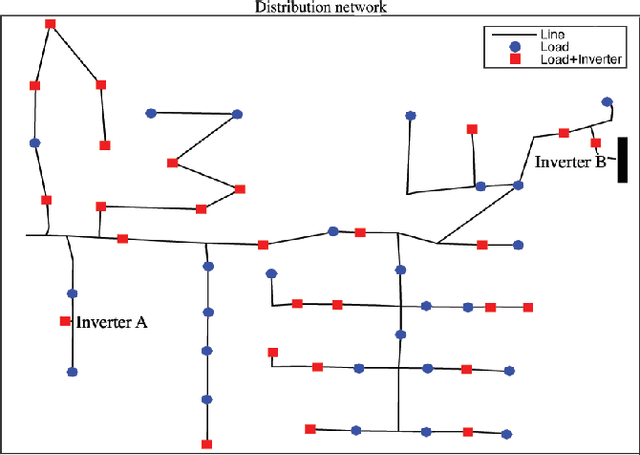
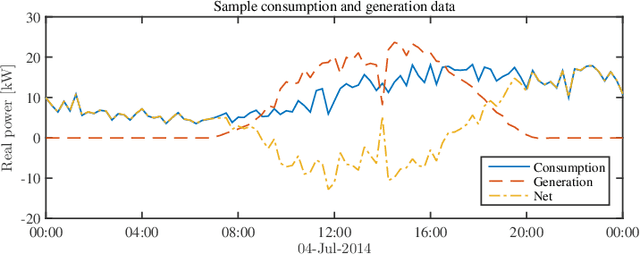
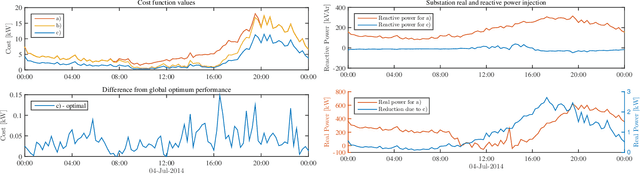
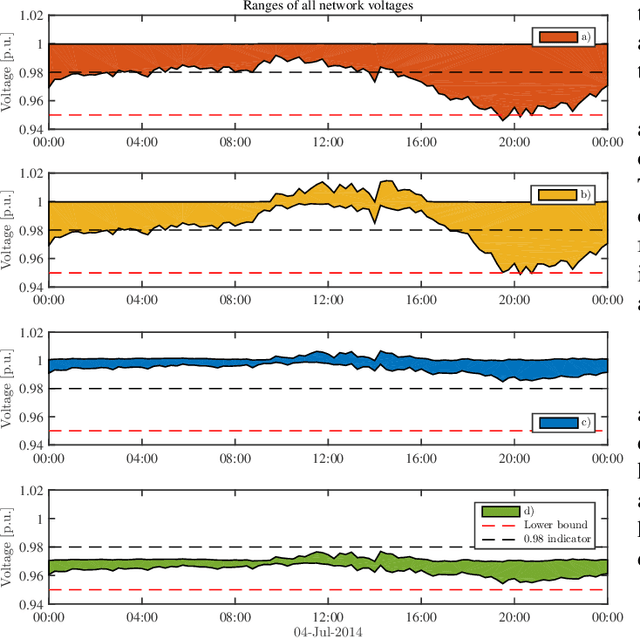
Electronic power inverters are capable of quickly delivering reactive power to maintain customer voltages within operating tolerances and to reduce system losses in distribution grids. This paper proposes a systematic and data-driven approach to determine reactive power inverter output as a function of local measurements in a manner that obtains near optimal results. First, we use a network model and historic load and generation data and do optimal power flow to compute globally optimal reactive power injections for all controllable inverters in the network. Subsequently, we use regression to find a function for each inverter that maps its local historical data to an approximation of its optimal reactive power injection. The resulting functions then serve as decentralized controllers in the participating inverters to predict the optimal injection based on a new local measurements. The method achieves near-optimal results when performing voltage- and capacity-constrained loss minimization and voltage flattening, and allows for an efficient volt-VAR optimization (VVO) scheme in which legacy control equipment collaborates with existing inverters to facilitate safe operation of distribution networks with higher levels of distributed generation.

Data-Driven Decentralized Optimal Power Flow

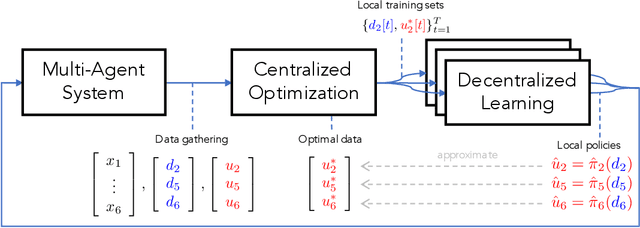
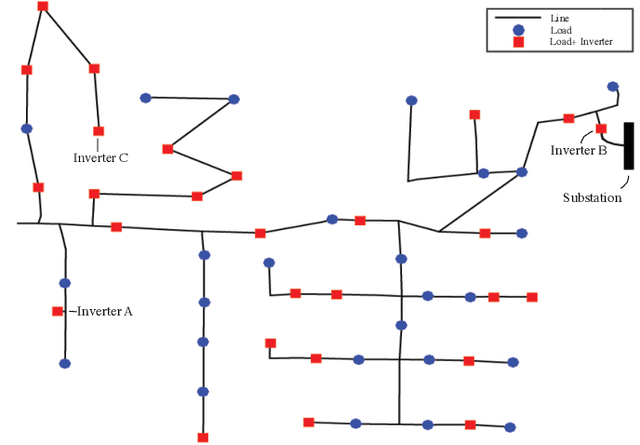
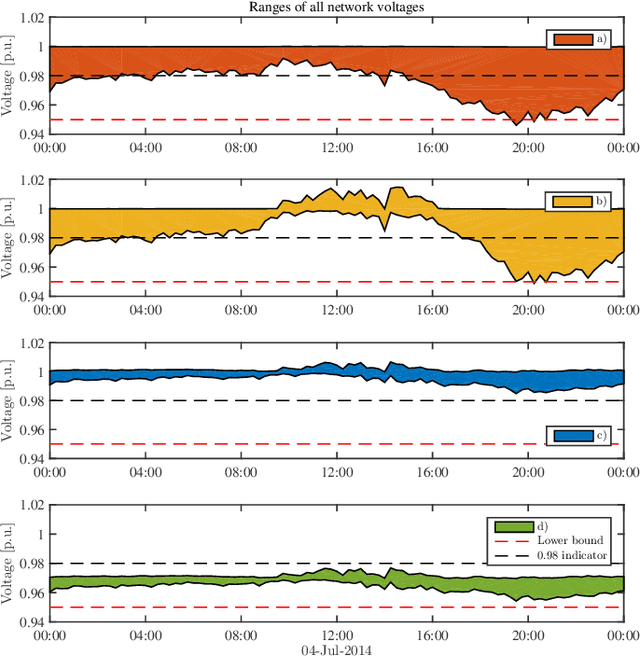
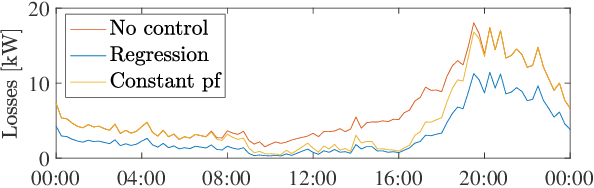
The implementation of optimal power flow (OPF) methods to perform voltage and power flow regulation in electric networks is generally believed to require communication. We consider distribution systems with multiple controllable Distributed Energy Resources (DERs) and present a data-driven approach to learn control policies for each DER to reconstruct and mimic the solution to a centralized OPF problem from solely locally available information. Collectively, all local controllers closely match the centralized OPF solution, providing near-optimal performance and satisfaction of system constraints. A rate distortion framework facilitates the analysis of how well the resulting fully decentralized control policies are able to reconstruct the OPF solution. Our methodology provides a natural extension to decide what buses a DER should communicate with to improve the reconstruction of its individual policy. The method is applied on both single- and three-phase test feeder networks using data from real loads and distributed generators. It provides a framework for Distribution System Operators to efficiently plan and operate the contributions of DERs to active distribution networks.