On Curvature-aided Incremental Aggregated Gradient Methods

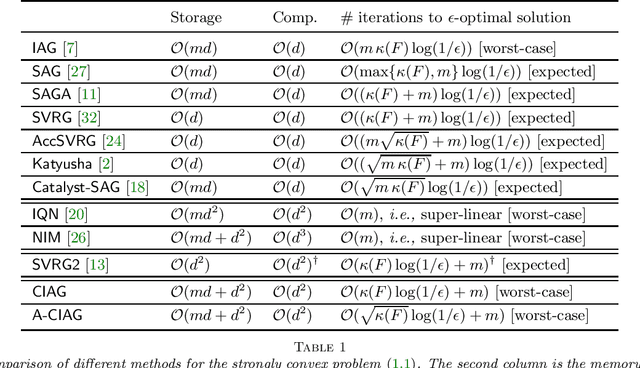
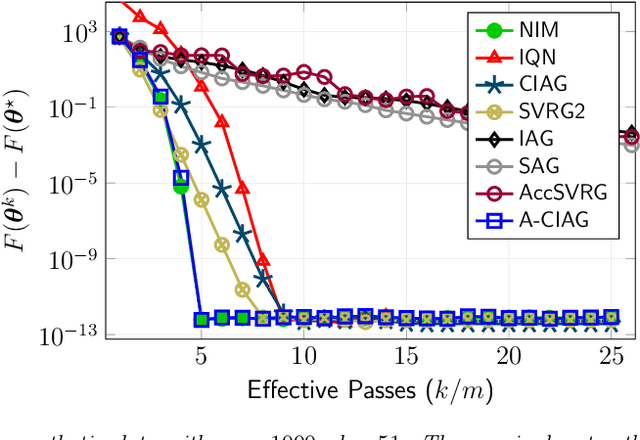
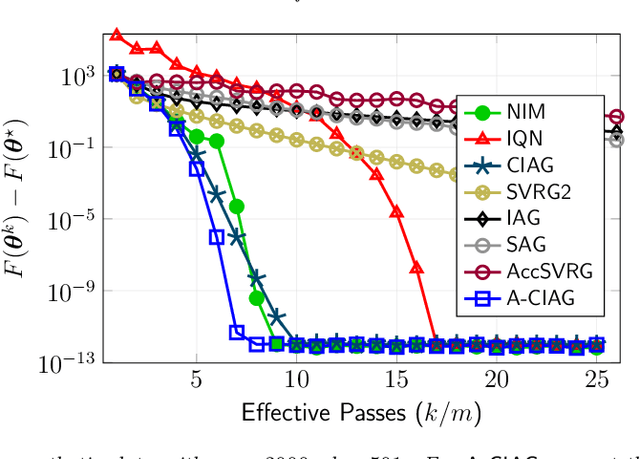
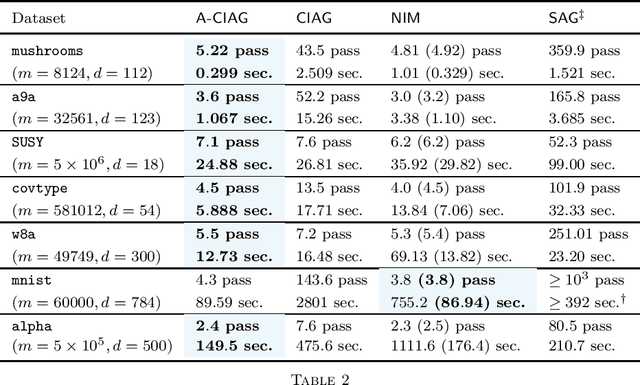
This paper studies an acceleration technique for incremental aggregated gradient methods which exploits curvature information for solving strongly convex finite sum optimization problems. These optimization problems of interest arise in large-scale learning applications relevant to machine learning systems. The proposed methods utilizes a novel curvature-aided gradient tracking technique to produce gradient estimates using the aids of Hessian information during computation. We propose and analyze two curvature-aided methods --- the first method, called curvature-aided incremental aggregated gradient (CIAG) method, can be developed from the standard gradient method and it computes an $\epsilon$-optimal solution using ${\cal O}( \kappa \log ( 1 / \epsilon ) )$ iterations for a small $\epsilon$; the second method, called accelerated CIAG (A-CIAG) method, incorporates Nesterov's acceleration into CIAG and requires ${\cal O}( \sqrt{\kappa} \log ( 1 / \epsilon ) )$ iterations for a small $\epsilon$, where $\kappa$ is the problem's condition number. Importantly, the asymptotic convergence rates above are the same as those of the full gradient and accelerated full gradient methods, respectively, and they are independent of the number of component functions involved. The proposed methods are significantly faster than the state-of-the-art methods, especially for large-scale problems with a massive amount of data. The source codes are available at https://github.com/hoitowai/ciag/