Support Estimation with Sampling Artifacts and Errors
Paper and Code
Jun 14, 2020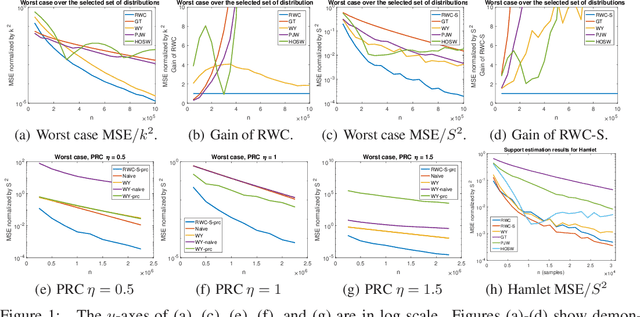
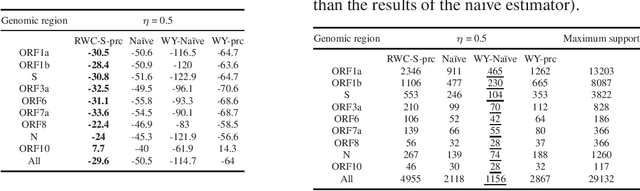
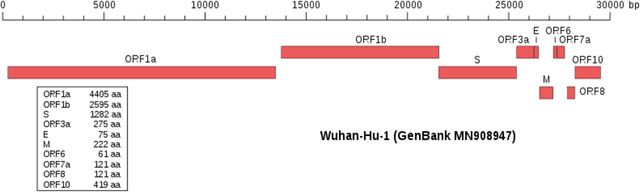
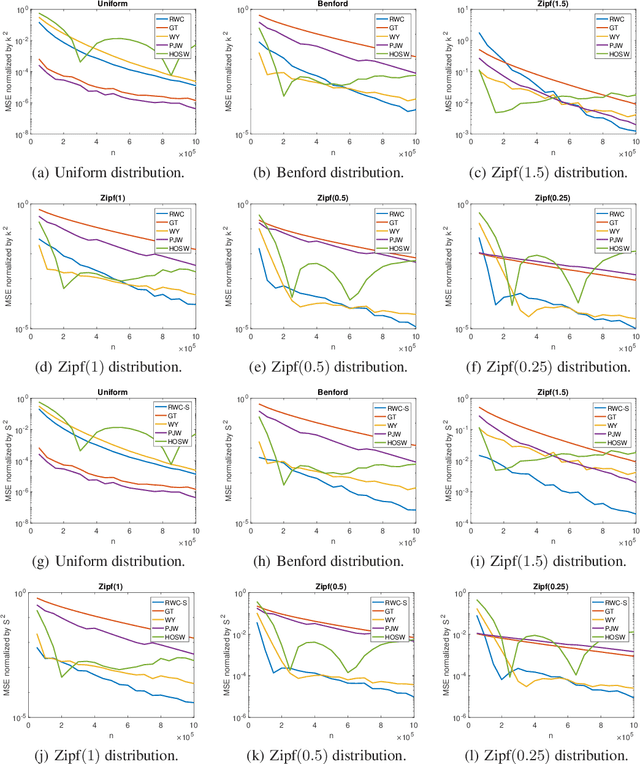
The problem of estimating the support of a distribution is of great importance in many areas of machine learning, computer science, physics and biology. Most of the existing work in this domain has focused on settings that assume perfectly accurate sampling approaches, which is seldom true in practical data science. Here we introduce the first known approach to support estimation in the presence of sampling artifacts and errors where each sample is assumed to arise from a Poisson repeat channel which simultaneously captures repetitions and deletions of samples. The proposed estimator is based on regularized weighted Chebyshev approximations, with weights governed by evaluations of so-called Touchard (Bell) polynomials. The supports in the presence of sampling artifacts are calculated using discretized semi-infite programming methods. The estimation approach is tested on synthetic and textual data, as well as on GISAID data collected to address a new problem in computational biology: mutational support estimation in genes of the SARS-Cov-2 virus. In the later setting, the Poisson channel captures the fact that many individuals are tested multiple times for the presence of viral RNA, thereby leading to repeated samples, while other individual's results are not recorded due to test errors. For all experiments performed, we observed significant improvements of our integrated methods compared to those obtained through adequate modifications of state-of-the-art noiseless support estimation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge