Convergence and Privacy of Decentralized Nonconvex Optimization with Gradient Clipping and Communication Compression

Achieving communication efficiency in decentralized machine learning has been attracting significant attention, with communication compression recognized as an effective technique in algorithm design. This paper takes a first step to understand the role of gradient clipping, a popular strategy in practice, in decentralized nonconvex optimization with communication compression. We propose PORTER, which considers two variants of gradient clipping added before or after taking a mini-batch of stochastic gradients, where the former variant PORTER-DP allows local differential privacy analysis with additional Gaussian perturbation, and the latter variant PORTER-GC helps to stabilize training. We develop a novel analysis framework that establishes their convergence guarantees without assuming the stringent bounded gradient assumption. To the best of our knowledge, our work provides the first convergence analysis for decentralized nonconvex optimization with gradient clipping and communication compression, highlighting the trade-offs between convergence rate, compression ratio, network connectivity, and privacy.

SoteriaFL: A Unified Framework for Private Federated Learning with Communication Compression

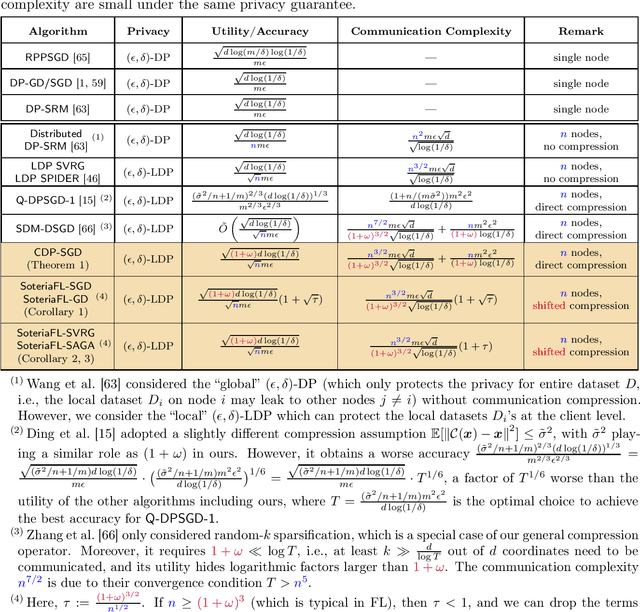
To enable large-scale machine learning in bandwidth-hungry environments such as wireless networks, significant progress has been made recently in designing communication-efficient federated learning algorithms with the aid of communication compression. On the other end, privacy-preserving, especially at the client level, is another important desideratum that has not been addressed simultaneously in the presence of advanced communication compression techniques yet. In this paper, we propose a unified framework that enhances the communication efficiency of private federated learning with communication compression. Exploiting both general compression operators and local differential privacy, we first examine a simple algorithm that applies compression directly to differentially-private stochastic gradient descent, and identify its limitations. We then propose a unified framework SoteriaFL for private federated learning, which accommodates a general family of local gradient estimators including popular stochastic variance-reduced gradient methods and the state-of-the-art shifted compression scheme. We provide a comprehensive characterization of its performance trade-offs in terms of privacy, utility, and communication complexity, where SoteraFL is shown to achieve better communication complexity without sacrificing privacy nor utility than other private federated learning algorithms without communication compression.

BEER: Fast $O$ Rate for Decentralized Nonconvex Optimization with Communication Compression

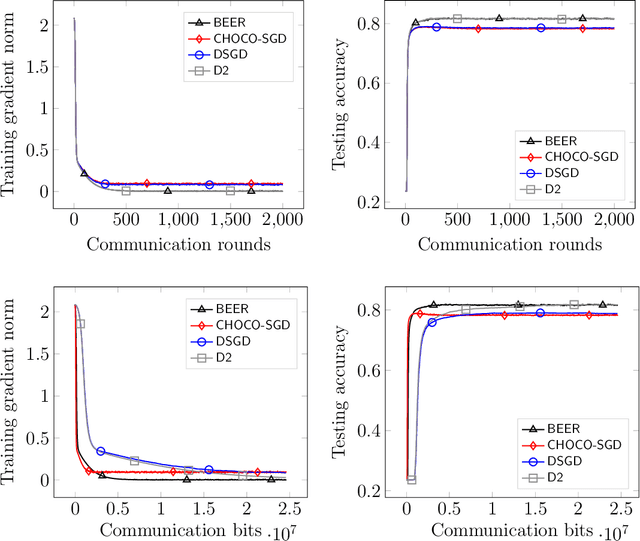
Communication efficiency has been widely recognized as the bottleneck for large-scale decentralized machine learning applications in multi-agent or federated environments. To tackle the communication bottleneck, there have been many efforts to design communication-compressed algorithms for decentralized nonconvex optimization, where the clients are only allowed to communicate a small amount of quantized information (aka bits) with their neighbors over a predefined graph topology. Despite significant efforts, the state-of-the-art algorithm in the nonconvex setting still suffers from a slower rate of convergence $O((G/T)^{2/3})$ compared with their uncompressed counterpart, where $G$ measures the data heterogeneity across different clients, and $T$ is the number of communication rounds. This paper proposes BEER, which adopts communication compression with gradient tracking, and shows it converges at a faster rate of $O(1/T)$. This significantly improves over the state-of-the-art rate, by matching the rate without compression even under arbitrary data heterogeneity. Numerical experiments are also provided to corroborate our theory and confirm the practical superiority of BEER in the data heterogeneous regime.

DESTRESS: Computation-Optimal and Communication-Efficient Decentralized Nonconvex Finite-Sum Optimization

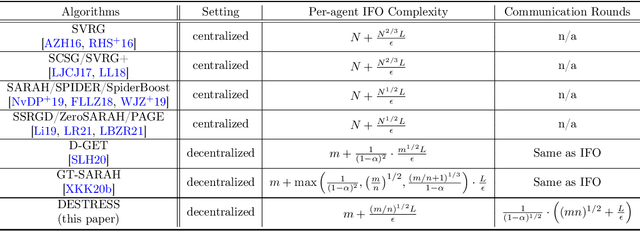
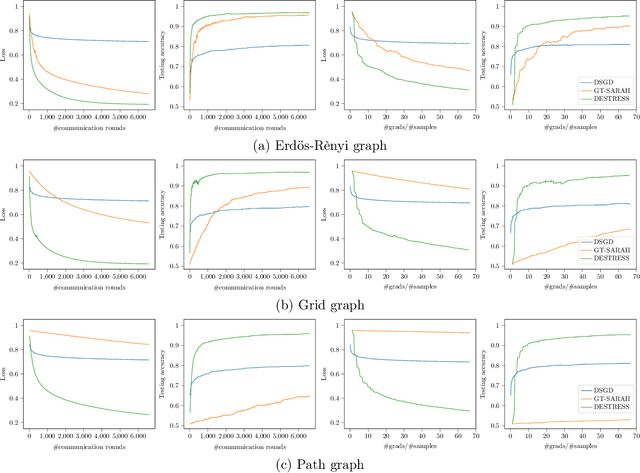
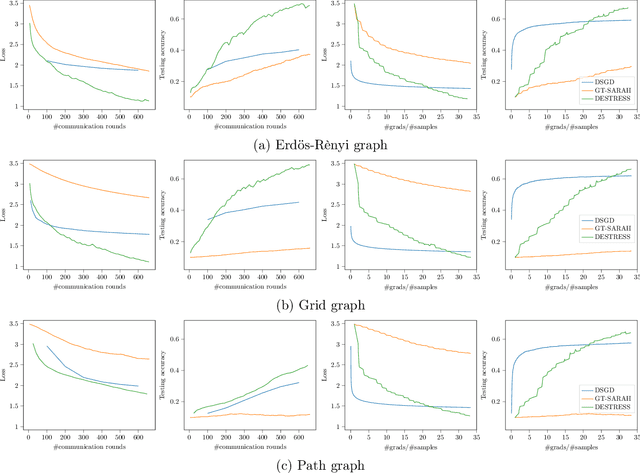
Emerging applications in multi-agent environments such as internet-of-things, networked sensing, autonomous systems and federated learning, call for decentralized algorithms for finite-sum optimizations that are resource-efficient in terms of both computation and communication. In this paper, we consider the prototypical setting where the agents work collaboratively to minimize the sum of local loss functions by only communicating with their neighbors over a predetermined network topology. We develop a new algorithm, called DEcentralized STochastic REcurSive gradient methodS (DESTRESS) for nonconvex finite-sum optimization, which matches the optimal incremental first-order oracle (IFO) complexity of centralized algorithms for finding first-order stationary points, while maintaining communication efficiency. Detailed theoretical and numerical comparisons corroborate that the resource efficiencies of DESTRESS improve upon prior decentralized algorithms over a wide range of parameter regimes. DESTRESS leverages several key algorithm design ideas including stochastic recursive gradient updates with mini-batches for local computation, gradient tracking with extra mixing (i.e., multiple gossiping rounds) for per-iteration communication, together with careful choices of hyper-parameters and new analysis frameworks to provably achieve a desirable computation-communication trade-off.

NCH Sleep DataBank: A Large Collection of Real-world Pediatric Sleep Studies

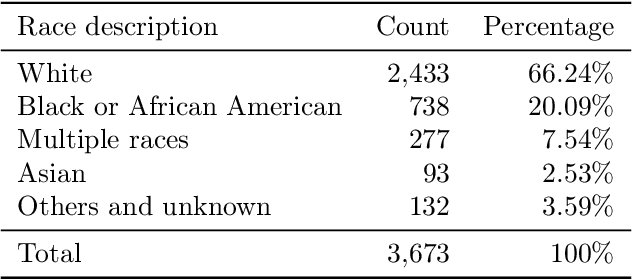
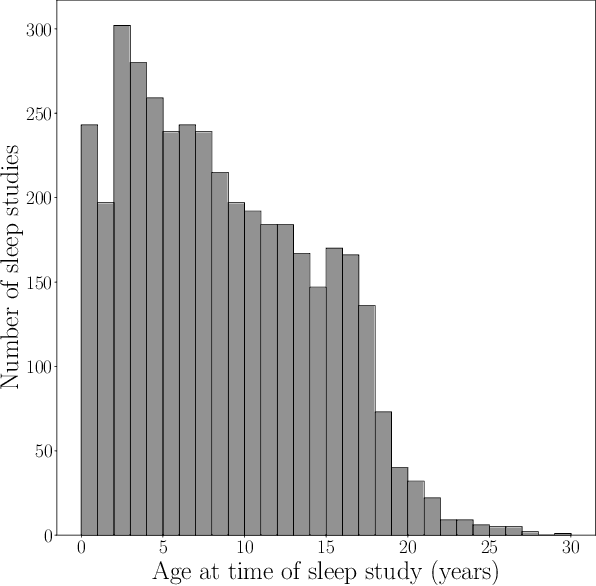
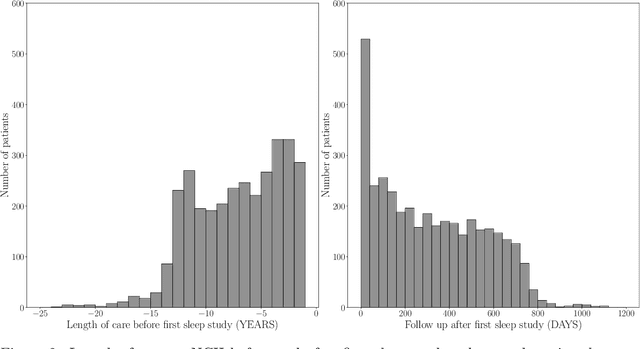
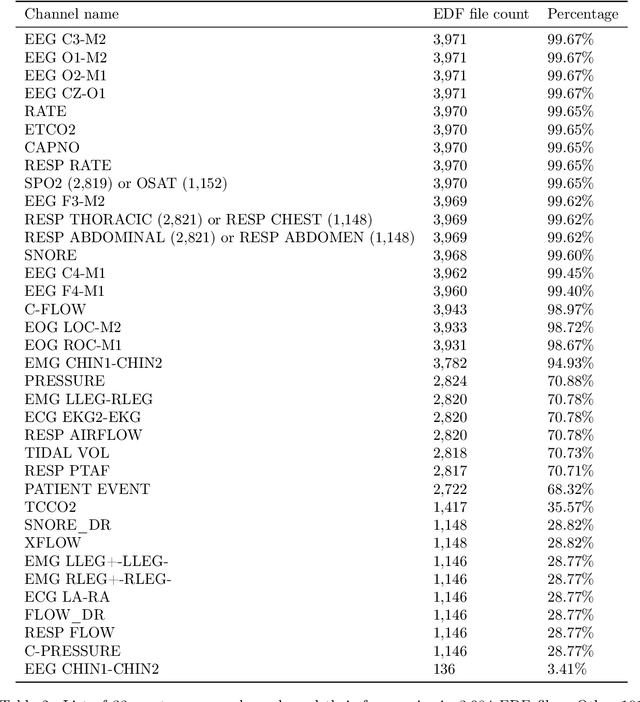
Despite being crucial to health and quality of life, sleep -- especially pediatric sleep -- is not yet well understood. This is exacerbated by lack of access to sufficient pediatric sleep data with clinical annotation. In order to accelerate research on pediatric sleep and its connection to health, we create the Nationwide Children's Hospital (NCH) Sleep DataBank and publish it at the National Sleep Research Resource (NSRR), which is a large sleep data common with physiological data, clinical data, and tools for analyses. The NCH Sleep DataBank consists of 3,984 polysomnography studies and over 5.6 million clinical observations on 3,673 unique patients between 2017 and 2019 at NCH. The novelties of this dataset include: 1) large-scale sleep dataset suitable for discovering new insights via data mining, 2) explicit focus on pediatric patients, 3) gathered in a real-world clinical setting, and 4) the accompanying rich set of clinical data. The NCH Sleep DataBank is a valuable resource for advancing automatic sleep scoring and real-time sleep disorder prediction, among many other potential scientific discoveries.

Communication-Efficient Distributed Optimization in Networks with Gradient Tracking

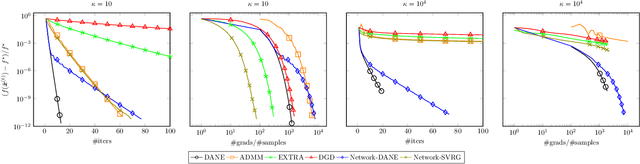
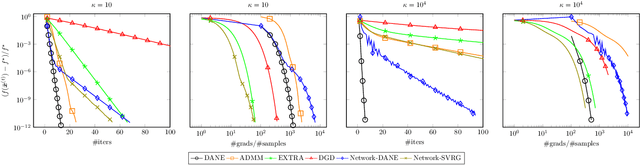
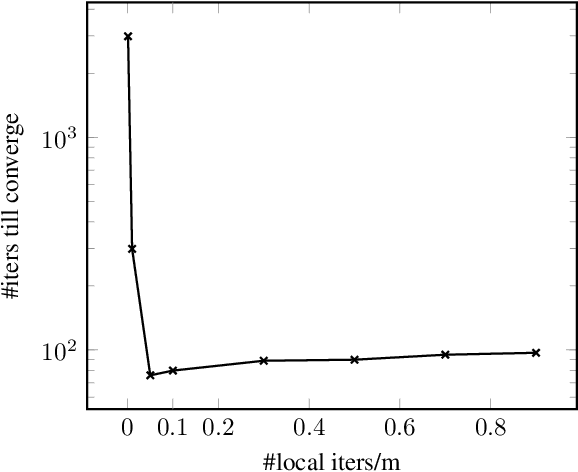
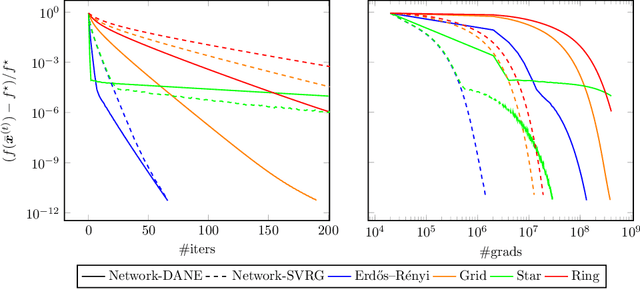
There is a growing interest in large-scale machine learning and optimization over decentralized networks, e.g. in the context of multi-agent learning and federated learning. Due to the imminent need to alleviate the communication burden, the investigation of communication-efficient distributed optimization algorithms --- particularly for empirical risk minimization --- has flourished in recent years. A large faction of these algorithms have been developed for the master/slave setting, relying on the presence of a central parameter server that can communicate with all agents. This paper focuses on distributed optimization over the network-distributed or the decentralized setting, where each agent is only allowed to aggregate information from its neighbors over a network (namely, no centralized coordination is present). By properly adjusting the global gradient estimate via a tracking term, we develop a communication-efficient approximate Newton-type method, called Network-DANE, which generalizes DANE [Shamir et al., 2014] for decentralized networks. We establish linear convergence of Network-DANE for quadratic losses, which shed light on the impact of data homogeneity and network connectivity upon the rate of convergence. Our key algorithmic ideas can be applied, in a systematic manner, to obtain decentralized versions of other master/slave distributed algorithms. A notable example is our development of Network-SVRG, which employs stochastic variance reduction [Johnson and Zhang, 2013] at each agent to accelerate local computation. The proposed algorithms are built upon the primal formulation without resorting to the dual. Numerical evidence is provided to demonstrate the appealing performance of our algorithms over competitive baselines, in terms of both communication and computation efficiency.

Nonparametric Density Estimation under Adversarial Losses

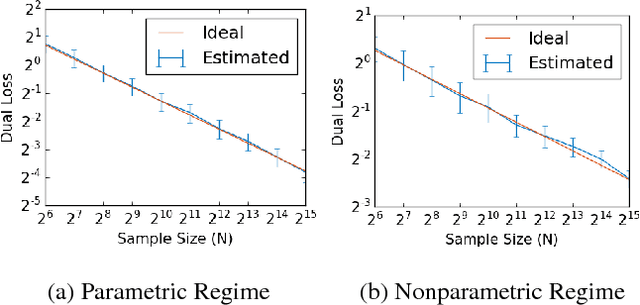
We study minimax convergence rates of nonparametric density estimation under a large class of loss functions called "adversarial losses", which, besides classical $\mathcal{L}^p$ losses, includes maximum mean discrepancy (MMD), Wasserstein distance, and total variation distance. These losses are closely related to the losses encoded by discriminator networks in generative adversarial networks (GANs). In a general framework, we study how the choice of loss and the assumed smoothness of the underlying density together determine the minimax rate. We also discuss implications for training GANs based on deep ReLU networks, and more general connections to learning implicit generative models in a minimax statistical sense.

Predictive State Recurrent Neural Networks

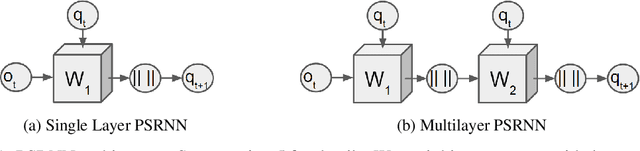
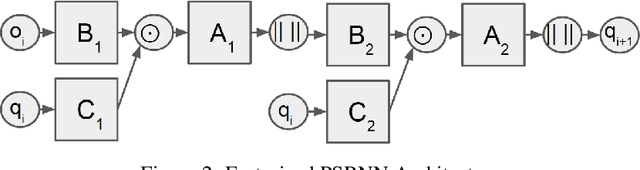
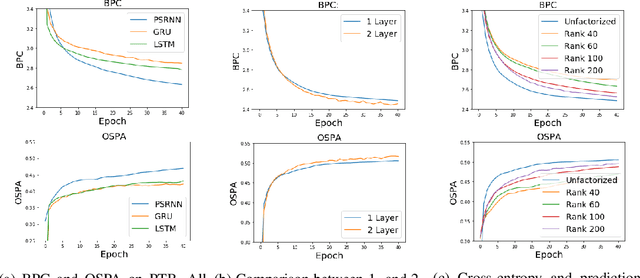
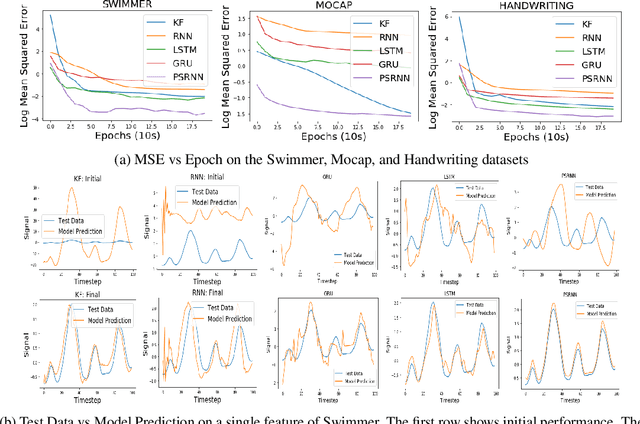
We present a new model, Predictive State Recurrent Neural Networks (PSRNNs), for filtering and prediction in dynamical systems. PSRNNs draw on insights from both Recurrent Neural Networks (RNNs) and Predictive State Representations (PSRs), and inherit advantages from both types of models. Like many successful RNN architectures, PSRNNs use (potentially deeply composed) bilinear transfer functions to combine information from multiple sources. We show that such bilinear functions arise naturally from state updates in Bayes filters like PSRs, in which observations can be viewed as gating belief states. We also show that PSRNNs can be learned effectively by combining Backpropogation Through Time (BPTT) with an initialization derived from a statistically consistent learning algorithm for PSRs called two-stage regression (2SR). Finally, we show that PSRNNs can be factorized using tensor decomposition, reducing model size and suggesting interesting connections to existing multiplicative architectures such as LSTMs. We applied PSRNNs to 4 datasets, and showed that we outperform several popular alternative approaches to modeling dynamical systems in all cases.